题目内容
如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的序号是 .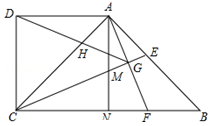
①②③④.
解析试题分析:如解答图所示:
结论①正确:证明△ACM≌△ABF即可;
结论②正确:由△ACM≌△ABF得∠2=∠4,进而得∠4+∠6=90°,即CE⊥AF;
结论③正确:证法一:利用四点共圆;证法二:利用三角形全等;
结论④正确:证法一:利用四点共圆;证法二:利用三角形全等.
试题解析:(1)结论①正确.理由如下:
∵∠1=∠2,∠1+∠CMN=90°,∠2+∠6=90°,
∴∠6=∠CMN,又∵∠5=∠CMN,
∴∠5=∠6,
∴AM=AE=BF.
易知ADCN为正方形,△ABC为等腰直角三角形,
∴AB=AC.
在△ACM与△ABF中, ,
,
∴△ACM≌△ABF(SAS),
∴CM=AF;
(2)结论②正确.理由如下:
∵△ACM≌△ABF,
∴∠2=∠4,
∵∠2+∠6=90°,
∴∠4+∠6=90°,
∴CE⊥AF;
(3)结论③正确.理由如下:
证法一:∵CE⊥AF,
∴∠ADC+∠AGC=180°,
∴A、D、C、G四点共圆,
∴∠7=∠2,
∵∠2=∠4,
∴∠7=∠4,
又∵∠DAH=∠B=45°,
∴△ABF∽△DAH;
证法二:∵CE⊥AF,∠1=∠2,
∴△ACF为等腰三角形,AC=CF,点G为AF中点.
在Rt△ANF中,点G为斜边AF中点,
∴NG=AG,
∴∠MNG=∠3,
∴∠DAG=∠CNG.
在△ADG与△NCG中, ,
,
∴△ADG≌△NCG(SAS),
∴∠7=∠1,
又∵∠1=∠2=∠4,
∴∠7=∠4,
又∵∠DAH=∠B=45°,
∴△ABF∽△DAH;
(4)结论④正确.理由如下:
证法一:∵A、D、C、G四点共圆,
∴∠DGC=∠DAC=45°,∠DGA=∠DCA=45°,
∴∠DGC=∠DGA,即GD平分∠AGC.
证法二:∵AM=AE,CE⊥AF,
∴∠3=∠4,又∠2=∠4,∴∠3=∠2
则∠CGN=180°-∠1-90°-∠MNG=180°-∠1-90°-∠3=90°-∠1-∠2=45°.
∵△ADG≌△NCG,
∴∠DGA=∠CGN=45°= ∠AGC,
∠AGC,
∴GD平分∠AGC.
综上所述,正确的结论是:①②③④,共4个.
考点:1.相似三角形的判定与性质;2.全等三角形的判定与性质.

如图,△ABC中,DE∥BC,DE=1,AD=2,DB=3,则BC的长是
A. | B. | C. | D. |
 =
= ,则CF的长为 _________ .
,则CF的长为 _________ .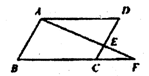

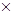 1.6m,位于AB中点处的台球E沿直线向BC边上的点F运动,经BC边反弹后恰好落入点D处的袋子中,则BF的长度为 m.
1.6m,位于AB中点处的台球E沿直线向BC边上的点F运动,经BC边反弹后恰好落入点D处的袋子中,则BF的长度为 m.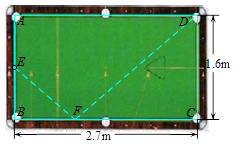
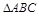 ∽
∽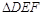 ,且相似比为
,且相似比为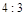 ,若
,若 边上的中线
边上的中线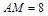 ,则
,则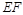 边上的中线
边上的中线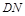 = .
= .