Question

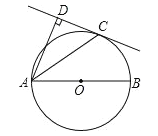
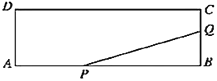
【题目】如图，在矩形中，边长，，两动点、分别从、同时出发，点从沿向匀速运动，每秒，点从沿向匀速运动，每秒，两点、中有一点到达矩形的顶点则运动停止.设运动时间为秒，的面积为

（1）求与的函数关系式，并写出的取值范围；

（2）当、两点运动多少秒时，的面积为；

（3）当取何值时，的面积最大？并求出其最大面积.

Answer 1

【答案】(1) ，;(2)当、两点运动2秒时，的面积为;(3)当时，的面积最大，最大面积为

【解析】

（1）根据题意可知，，由矩形面积公式即可求出面积与的函数关系式，根据BC的长求出x的取值；

（2）令y=14即可求出x的值，根据x的取值范围即可得出答案；

（3）根据二次函数的图像与性质即可求出最值．

解：（1）在矩形中，

∵，，，

，，

∴

∵4÷1=4（秒）

∴的取值范围：．

（2）由（1）知：

∴

∴，，又∵

∴，应取.

∴当、两点运动2秒时，的面积为．

（3）∵

，开口向下，对称轴

当时，随的增大而增大.

又∵

∴当时，

∴当时，的面积最大，最大面积为．