题目内容
【题目】在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是边
是边![]() 上一点,
上一点,![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,交
,交![]() 边于点
边于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,![]() 分别交
分别交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)设![]() ,求
,求![]() 关于
关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(3)当![]() 是以
是以![]() 为腰的等腰三角形时,求线段
为腰的等腰三角形时,求线段![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)只要证明△OBD∽△NED,即可解决问题;
(2)由tan∠DBC=![]() ,又因为
,又因为![]() ,可得
,可得![]() ,由此即可解决问题;
,由此即可解决问题;
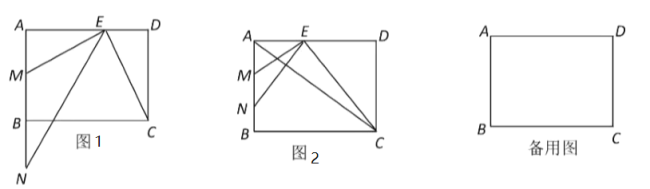
(3)分两种情形:①如图21中,当DE=DF时,②如图22中,当DE=EF时,分别求解即可解决问题.
(1)证明:如图1中,
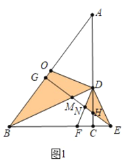
∵OD⊥DF,BD⊥DE,
∴∠ODF=∠BDE=90![]() ,
,
∴∠ODB=∠NDE,
∵EG⊥AB,
∴∠BGM=∠MDE=90![]() ,
,
∵∠BMG=∠EMD,
∴OBD=∠DEN,
∴△OBD∽△NED,
∴![]() .
.
(2)解:如图1中,∵∠BCD=∠BDE=90![]() ,
,
∴tan∠DBC=![]() ,
,
∵![]() ,
,
∴![]() ,
,
在Rt△ABC中,AB=![]() =
=![]() =5,
=5,
∴OB=OA=2.5,
∴![]() ,
,
∴y=![]() x,
x,
∵点![]() 是
是![]() 的中点,
的中点,![]() ,交
,交![]() 边于点
边于点![]() ,
,![]() ,
,
∴0<CD≤2,即定义域为:0<x≤2;
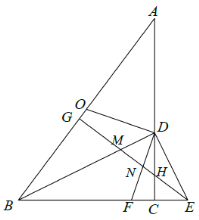
(3)解:①如图21中,当DE=DF时,作OK⊥AC于K,设CD=x.
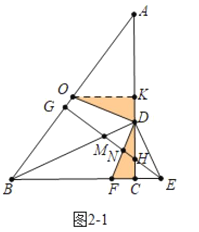
∵∠OKD=∠DCF=∠ODF=90![]() ,
,
∴∠ODK+∠KOD=90![]() ,∠ODK+∠CDF=90
,∠ODK+∠CDF=90![]() ,
,
∴∠DOK=∠CDF,
∴△OKD∽△DCF,
∴![]() ,
,
∴![]() ,
,
∴CF=![]() x(2x),
x(2x),
∵DF=DE,DC⊥EF,
∴∠CDE=∠CDF,
∵∠CDE+∠CDB=90![]() ,∠CBD+∠CDB=90
,∠CBD+∠CDB=90![]() ,
,
∴∠CDE=∠CBD=∠CDF,
∵∠DCF=∠DCB=90![]() ,
,
∴△DCF∽△BCD,
∴![]() ,
,
∴CD2=CFCB,
∴x2=2x(2x),
解得x=![]() 或0(舍弃)
或0(舍弃)
∴CD=![]() ;
;
②如图22中,当DE=EF时,设CD=x,
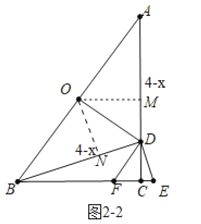
∵ED=EF,
∴∠EDF=∠EFD,
∴∠EDC+∠CDF=∠DBC+∠BDF,
∵∠EDC=∠DBC,
∴∠CDF=∠BDF,
∵∠CDF+∠ADO=90![]() ,∠BDF+∠BDO=90
,∠BDF+∠BDO=90![]() ,
,
∴∠ADO=∠BDO,
∵AO=OB,
作OM⊥AD于M,ON⊥BD于N,则OM=ON,
∵OA=OB,∠AMO=∠ONB=90![]() ,
,
∴Rt△AOM≌△BON(HL),
∴∠A=∠ABD,
∴DA=DB,
∴DA=DB=4x,
在Rt△BCD中,∵BD2=CD2+BC2,
∴(4x)2=x2+32,
∴x=![]() ,
,
∴CD=![]() .
.
综上所述,CD的长为![]() 或
或![]() .
.

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】已知抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x与纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … |
| ﹣4 |
| ﹣4 |
| 0 |
| … |
(1)求该抛物线的表达式;
(2)已知点E(4, y)是该抛物线上的点,点E关于抛物线的对称轴对称的点为点F,求点E和点F的坐标.