题目内容
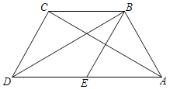
【题目】如图,AD∥BC,连接BD,点E在BC上,点F在DC上,连接EF,且∠1=∠2.

(1)求证:EF∥BD;
(2)若BD平分∠ABC,∠A=130°,∠C=70°,求∠CFE的度数.
【答案】(1)证明见解析;(2)∠CFE=85°.
【解析】
(1)由AD∥BC知∠1=∠3,结合∠1=∠2得∠3=∠2,据此即可得证;
(2)由AD∥BC、∠A=130°知∠ABC=50°,再根据平分线定义及BD∥EF知∠3=∠2=25°,由三角形的内角和定理可得答案.
解:(1)如图,
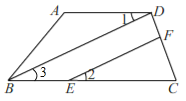
∵AD∥BC(已知),
∴∠1=∠3(两直线平行,内错角相等).
∵∠1=∠2,
∴∠3=∠2(等量代换).
∴EF∥BD(同位角相等,两直线平行).
(2)解:∵AD∥BC(已知),
∴∠ABC+∠A=180°(两直线平行,同旁内角互补).
∵∠A=130°(已知),
∴∠ABC=50°.
∵BD平分∠ABC(已知),
![]() ,
,
∴∠2=∠3=25°.
∵在△CFE中,∠CFE+∠2+∠C=180°(三角形内角和定理),∠C=70°,
∴∠CFE=85°.

练习册系列答案
相关题目