ЬтФПФкШн
ЁОЬтФПЁПаЁУїЁЂаЁЗМзівЛИіЁАХфЩЋЁБЕФгЮЯЗЃЎгвЭМЪЧСНИіПЩвдздгЩзЊЖЏЕФзЊХЬЃЌУПИізЊХЬБЛЗжГЩУцЛ§ЯрЕШЕФМИИіЩШаЮЃЌВЂЭПЩЯЭМжаЫљЪОЕФбеЩЋЃЎЭЌЪБзЊЖЏСНИізЊХЬЃЌШчЙћзЊХЬAзЊГіСЫКьЩЋЃЌзЊХЬBзЊГіСЫРЖЩЋЃЌЛђепзЊХЬAзЊГіСЫРЖЩЋЃЌзЊХЬBзЊГіСЫКьЩЋЃЌдђКьЩЋКЭРЖЩЋдквЛЦ№ХфГЩзЯЩЋЃЌетжжЧщПіЯТаЁЗМЛёЪЄЃЛЭЌбљЃЌРЖЩЋКЭЛЦЩЋдквЛЦ№ХфГЩТЬЩЋЃЌетжжЧщПіЯТаЁУїЛёЪЄЃЛдкЦфЫќЧщПіЯТЃЌдђаЁУїЁЂаЁЗМВЛЗжЪЄИКЃЎ
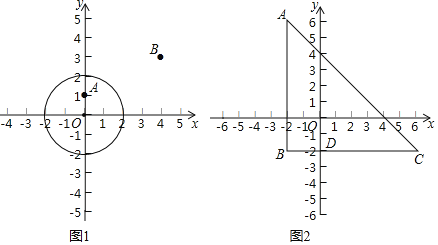
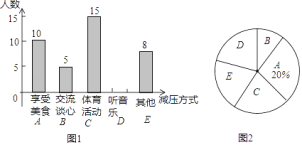
ЃЈ1ЃЉРћгУСаБэЛђЪїзДЭМЕФЗНЗЈБэЪОДЫгЮЯЗЫљгаПЩФмГіЯжЕФНсЙћЃЛ
ЃЈ2ЃЉДЫгЮЯЗЕФЙцдђЃЌЖдаЁУїЁЂаЁЗМЙЋЦНТ№ЃПЪдЫЕУїРэгЩЃЎ

ЁОД№АИЁП(1)ЫљгаПЩФмЕФНсЙћМћНтЮіЃЌЃЈ2ЃЉВЛЙЋЦН.
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉИљОнЬтвтЃЌгУСаБэЗЈНЋЫљгаПЩФмГіЯжЕФНсЙћЃЌМДПЩЕУД№АИЃЛ
ЃЈ2ЃЉгЩЃЈ1ЃЉЕФБэИёЃЌЗжЮіПЩФмЕУЕНзЯЩЋЁЂТЬЩЋЕФИХТЪЃЌЕУЕННсТлВЛЙЋЦНЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉгУСаБэЗЈНЋЫљгаПЩФмГіЯжЕФНсЙћБэЪОШчЯТЃКЫљгаПЩФмГіЯжЕФНсЙћЙВга12жжЃЎ
Кь | ЃЈКьЃЌКьЃЉ | ЃЈРЖЃЌКьЃЉ | ЃЈЛЦЃЌКьЃЉ |
РЖ | ЃЈКьЃЌРЖЃЉ | ЃЈРЖЃЌРЖЃЉ | ЃЈЛЦЃЌРЖЃЉ |
Кь | ЃЈКьЃЌКьЃЉ | ЃЈРЖЃЌКьЃЉ | ЃЈЛЦЃЌКьЃЉ |
ЛЦ | ЃЈКьЃЌЛЦЃЉ | ЃЈРЖЃЌЛЦЃЉ | ЃЈЛЦЃЌЛЦЃЉ |
Кь | РЖ | ЛЦ |
ЃЈ2ЃЉВЛЙЋЦНЃЎ
ЩЯУцЕШПЩФмГіЯжЕФ12жжНсЙћжаЃЌга3жжЧщПіПЩФмЕУЕНзЯЩЋЃЌЙЪХфГЩзЯЩЋЕФИХТЪЪЧ![]() ЃЌМДаЁУїЛёЪЄЕФИХТЪЪЧ
ЃЌМДаЁУїЛёЪЄЕФИХТЪЪЧ![]() ЃЛЕЋжЛга2жжЧщПіВХПЩФмЕУЕНТЬЩЋЃЌХфГЩТЬЩЋЕФИХТЪЪЧ
ЃЛЕЋжЛга2жжЧщПіВХПЩФмЕУЕНТЬЩЋЃЌХфГЩТЬЩЋЕФИХТЪЪЧ![]() ЃЌМДаЁЧПЛёЪЄЕФИХТЪЪЧ
ЃЌМДаЁЧПЛёЪЄЕФИХТЪЪЧ![]() ЃЎЖј
ЃЎЖј![]() ЃО
ЃО![]() ЃЌЙЪаЁЗМЛёЪЄЕФПЩФмадДѓЃЌетИіЁАХфЩЋЁБгЮЯЗЖдЫЋЗНЪЧВЛЙЋЦНЕФЃЎ
ЃЌЙЪаЁЗМЛёЪЄЕФПЩФмадДѓЃЌетИіЁАХфЩЋЁБгЮЯЗЖдЫЋЗНЪЧВЛЙЋЦНЕФЃЎ

 гХжЪПЮЬУПьРжГЩГЄЯЕСаД№АИ
гХжЪПЮЬУПьРжГЩГЄЯЕСаД№АИЁОЬтФПЁПдФЖСЯТСаВФСЯЃКгаетбљвЛИіЮЪЬтЃКЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() гаСНИіВЛЯрЕШЕФЧвЗЧСуЕФЪЕЪ§ИљЬНОП
гаСНИіВЛЯрЕШЕФЧвЗЧСуЕФЪЕЪ§ИљЬНОП![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ТњзуЕФЬѕМў.
ТњзуЕФЬѕМў.
аЁУїИљОнбЇЯАКЏЪ§ЕФОбщЃЌШЯЮЊПЩвдДгЖўДЮКЏЪ§ЕФНЧЖШПДвЛдЊЖўДЮЗНГЬЃЌЯТУцЪЧаЁУїЕФЬНОПЙ§ГЬЃКЂйЩшвЛдЊЖўДЮЗНГЬ![]() ЖдгІЕФЖўДЮКЏЪ§ЮЊ
ЖдгІЕФЖўДЮКЏЪ§ЮЊ![]() ЃЛ
ЃЛ
ЂкНшжњЖўДЮКЏЪ§ЭМЯѓЃЌПЩвдЕУЕНЯргІЕФвЛдЊЖўДЮжа![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ТњзуЕФЬѕМўЃЌСаБэШчЯТЃК
ТњзуЕФЬѕМўЃЌСаБэШчЯТЃК
ЗНГЬИљЕФМИКЮвтвхЃК
ЗНГЬСНИљЕФЧщПі | ЖдгІЕФЖўДЮКЏЪ§ЕФДѓжТЭМЯѓ |
|
ЗНГЬгаСНИіВЛЯрЕШЕФИКЪЕИљ |
|
|
____________ |
|
|
ЗНГЬгаСНИіВЛЯрЕШЕФе§ЪЕИљ | ____________ | ____________ |
ЃЈ1ЃЉВЮПМаЁУїЕФзіЗЈЃЌАбЩЯЪіБэИёВЙГфЭъећЃЛ
ЃЈ2ЃЉШєвЛдЊЖўДЮЗНГЬ![]() гавЛИіИКЪЕИљЃЌвЛИіе§ЪЕИљЃЌЧвИКЪЕИљДѓгк-1ЃЌЧѓЪЕЪ§
гавЛИіИКЪЕИљЃЌвЛИіе§ЪЕИљЃЌЧвИКЪЕИљДѓгк-1ЃЌЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.