Question

【题目】矩形的两条对角线的夹角为，对角线长为，则较短的边长为________．

Answer 1

【答案】

【解析】

根据题意画出对应图形，∠AOD=∠BOC=60°，则∠COD=120°＞∠AOD=60°，AD是该矩形较短的一边，根据矩形的性质：矩形的对角线相等且互相平分，所以有OA=OD=OC=OB=6，又因为∠AOD=∠BOC=60°，所以AD=OA=0D=6．

如下图所示：矩形ABCD，对角线AC=BD=12，∠AOD=∠BOC=60°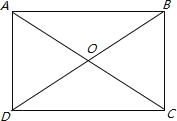

∵四边形ABCD是矩形
∴OA=OD=OC=OB=×12=6（矩形的对角线互相平分且相等）
又∵∠AOD=∠BOC=60°，
∴OA=OD=AD=6，
∵∠COD=120°＞∠AOD=60°
∴AD＜DC
所以该矩形较短的一边长为6，
故答案是：6．