题目内容
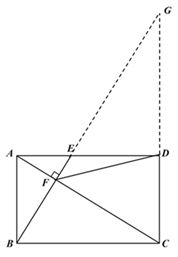
【题目】如图,已知矩形ABCD,点E为AD上一点,BE ⊥ AC于F点.

(1)若AE=![]() AD,△AEF的面积为1时,求△ABC的面积;
AD,△AEF的面积为1时,求△ABC的面积;
(2)若AD = 4,tan∠EAF =![]() ,求AF的长;
,求AF的长;
(3)若tan∠EAF =![]() ,连接DF,证明DF=AB.
,连接DF,证明DF=AB.
【答案】(1)12;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】分析:![]() 证明三角形相似,根据相似三角形的面积比等于相似比的平方即可求出.
证明三角形相似,根据相似三角形的面积比等于相似比的平方即可求出.
![]() 利用正切得到
利用正切得到![]() AB = DC = 2,tan∠ABF =
AB = DC = 2,tan∠ABF = ![]() ,即BF=2AF,用勾股定理即可求出
,即BF=2AF,用勾股定理即可求出![]() 的长.
的长.
![]() ∠EAF =∠ABF,tan∠EAF =
∠EAF =∠ABF,tan∠EAF =![]() ,可以得到
,可以得到![]() ,可以推出E为AD中点,
,可以推出E为AD中点,
延长BE、CD交于点G,易证△ABE ≌△DGE,即可证明.
详解:(1)∵四边形ABCD是矩形
∴AD = BC,![]() ,
,
∴![]() ,
,
∵S△AEF = 1,
∴S△CBF = 9S△AEF = 9,S△ABF = 3S△AEF = 3,
∴S△ABC = S△ABF + S△CBF = 12.
(2)∵AD = 4,tan∠EAF =![]() ,
,
∴![]()
∴AB = DC = 2,
∵∠EAF + ∠BAF = 90°,∠BAF + ∠ABF = 90° ,
∴∠EAF = ∠ABF,
∴ tan∠ABF = ![]() ,即BF=2AF,
,即BF=2AF,
∵AF2 + BF2 = AB2,
∴![]()
∴AF =![]() .
.
(3)∵∠EAF =∠ABF,tan∠EAF =![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴ ![]() ,
,
∴E为AD中点,
延长BE、CD交于点G,
易证△ABE ≌ △DGE,
∴DG = AB = DC,
∴DF = DC.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目