题目内容
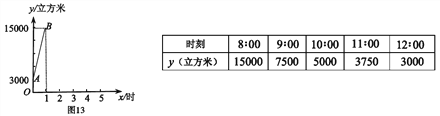
【题目】为节约能源，某市众多车主响应号召，将燃油汽车改装为天然气汽车.某日上午7:00－8:00， 燃气公司给该城西加气站的储气罐加气，8:00 加气站开始为前来的车辆加气. 储气罐内的天然气总量y（立方米）随加气时间x（时）的变化而变化.
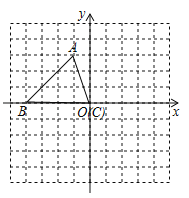
（1）在7:00－8:00 范围内，y 随x的变化情况如图13 所示，求y 关于x 的函数解析式；
（2）在8:00－12:00 范围内，y 的变化情况如下表所示，请写出一个符合表格中数据的y 关于x 的函数解析式，依此函数解析式，判断上午9：05 到9：20 能否完成加气950 立方米的任务，并说明理由.
【答案】（1）在8:00－8:00范围内，y关于x的函数解析式为：y＝12000x＋3000（0≤x≤1）
（2）上午9：05到9：20不能完成加气950立方米的任务
【解析】试题分析：（1）根据图象发现是一次函数,把点A（0，3000），B（1，15000）代入即可求解;(2)因为y随x的增大而减小,所以猜测是反比例函数y＝
（1≤x≤3）,根据x＝1时，y＝15000，即上午8:00，x与y的值满足解析式,再验证其余时间是否满足, 把上午9：05即x＝2
时代入y＝
（1≤x≤3）求出,再把上午9：20即x＝2
时代入y＝
（1≤x≤3）求出,两结果之差和950进行比较就能得出结果.
试题解析：
（1）设直线AB的解析式为y＝kx＋b，
把点A（0，3000），B（1，15000）分别代入，得
k＝12000，b＝3000．
在8:00－8:30范围内，y关于x的函数解析式为：y＝12000x＋3000（0≤x≤1）．
（2）解法一：函数解析式为：y＝
（1≤x≤3）．
验证如下：
当x＝1时，y＝15000，即上午8:00，x与y的值满足解析式．
同理，表格数据所对应的x与y的值都满足解析式.
当上午9：05即x＝2
时，y＝7200立方米．
当上午9：20即x＝2
时，y＝
立方米．
∵ 7200－
＝
，
又∵
＜950，
∴ 上午9：05到9：20不能完成加气950立方米的任务.
解法二：函数解析式为：y＝
（1≤x≤3）．
验证如下：
当x＝1时，y＝15000，即上午8:00，x与y的值满足解析式．
同理，表格数据所对应的x与y的值都满足解析式.
当上午9：05即x＝2
时，y＝7200立方米．
7200－950＝6250．
当y＝6250立方米，x＝2
时．
即到上午9：24才可完成加气任务．
所以上午9：05到9：20不能完成加气950立方米的任务.
金牌教辅培优优选卷期末冲刺100分系列答案
