题目内容
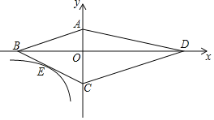
【题目】如图,在![]() ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边
ABC中,AC=BC,∠ACB=120°,点D是AB边上一点,连接CD,以CD为边作等边![]() CDE.
CDE.
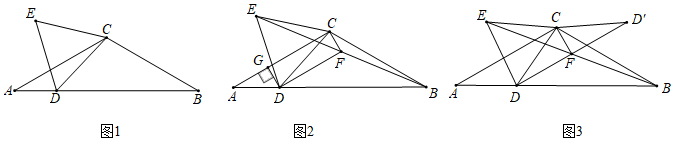
(1)如图1,若∠CDB=45°,AB=6,求等边![]() CDE的边长;
CDE的边长;
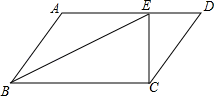
(2)如图2,点D在AB边上移动过程中,连接BE,取BE的中点F,连接CF,DF,过点D作DG⊥AC于点G.
①求证:CF⊥DF;
②如图3,将![]() CFD沿CF翻折得
CFD沿CF翻折得![]() CF
CF![]() ,连接B
,连接B![]() ,直接写出
,直接写出![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)①证明见解析;②
;(2)①证明见解析;②![]() .
.
【解析】
(1)过点C作CH⊥AB于点 H,由等腰三角形的性质和直角三角形的性质可得∠A=∠B=30°,AH=BH=3,CH=![]() =
=![]() ,由∠CDB=45°,可得CD=
,由∠CDB=45°,可得CD=![]() CH=
CH=![]() ;
;
(2)①延长BC到N,使CN=BC,由“SAS”可证![]() CEN≌
CEN≌![]() CDA,可得EN=AD,∠N=∠A=30°,由三角形中位线定理可得CF∥EN,CF=
CDA,可得EN=AD,∠N=∠A=30°,由三角形中位线定理可得CF∥EN,CF=![]() EN,可得∠BCF=∠N=30°,可证DG=CF,DG∥CF,即可证四边形CFDG是矩形,可得结论;
EN,可得∠BCF=∠N=30°,可证DG=CF,DG∥CF,即可证四边形CFDG是矩形,可得结论;
②由“SAS”可证![]() EFD≌
EFD≌![]() BF
BF![]() ,可得B
,可得B![]() =DE,则当CD取最小值时,
=DE,则当CD取最小值时,![]() 有最小值,即可求解.
有最小值,即可求解.
解:(1)如图1,过点C作CH⊥AB于点 H,

∵AC=BC,∠ACB=120°,CH⊥AB,
∴∠A=∠B=30°,AH=BH=3,
在Rt![]() BCH中,tan∠B=
BCH中,tan∠B=![]() ,
,
∴tan30°=![]()
∴CH=![]() =
=![]() ,
,
∵∠CDH=45°,CH⊥AB,
∴∠CDH=∠DCH=45°,
∴DH=CH=![]() ,CD=
,CD=![]() CH=
CH=![]() ;
;
(2)①如图2,延长BC到N,使CN=BC,
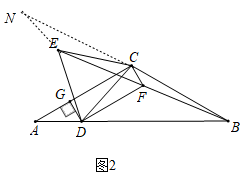
∵AC=BC,∠ACB=120°,
∴∠A=∠ABC=30°,∠NCA=60°,
∵![]() ECD是等边三角形,
ECD是等边三角形,
∴EC=CD,∠ECD=60°,
∴∠NCA=∠ECD,
∴∠NCE=∠DCA,
又∵CE=CD,AC=BC=CN,
∴![]() CEN≌
CEN≌![]() CDA(SAS),
CDA(SAS),
∴EN=AD,∠N=∠A=30°,
∵BC=CN,BF=EF,
∴CF∥EN,CF=![]() EN,
EN,
∴∠BCF=∠N=30°,
∴∠ACF=∠ACB﹣∠BCF=90°,
又∵DG⊥AC,
∴CF∥DG,
∵∠A=30°,DG⊥AC,
∴DG=![]() AD,
AD,
∴DG=CF,
∴四边形CFDG是平行四边形,
又∵∠ACF=90°,
∴四边形CFDG是矩形,
∴∠CFD=90°
∴CF⊥DF;
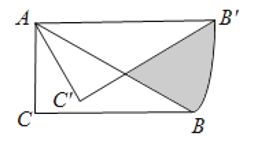
②如图3,连接B![]() ,
,
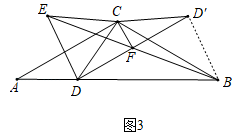
∵将![]() CFD沿CF翻折得
CFD沿CF翻折得![]() CF
CF![]() ,
,
∴CD=C![]() ,DF=
,DF=![]() F,∠CFD=∠CF
F,∠CFD=∠CF![]() =90°,
=90°,
又∵EF=BF,∠EFD=∠BF![]() ,
,
∴![]() EFD≌
EFD≌![]() BF
BF![]() (SAS),
(SAS),
∴B![]() =DE,
=DE,
∴B![]() =CD,
=CD,
∵当B![]() 取最小值时,
取最小值时,![]() 有最小值,
有最小值,
∴当CD取最小值时,![]() 有最小值,
有最小值,
∵当CD⊥AB时,CD有最小值,
∴AD=![]() CD,AB=2AD=2
CD,AB=2AD=2![]() CD,
CD,
∴![]() 最小值=
最小值=![]() .
.

 习题精选系列答案
习题精选系列答案