题目内容
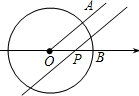 如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )
如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠AOB=45°,点P在数轴上运动,若过点P且与OA平行的直线与⊙O有公共点,设OP=x,则x的取值范围是( )A、O<x≤
| ||||
B、-
| ||||
| C、-1≤x≤1 | ||||
D、x>
|
分析:根据题意,知直线和圆有公共点,则相切或相交.相切时,设切点为C,连接OC.根据等腰直角三角形的直角边是圆的半径1,求得斜边是
.所以x的取值范围是0≤x≤
.
| 2 |
| 2 |
解答: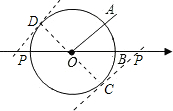 解:设切点为C,连接OC,则
解:设切点为C,连接OC,则
圆的半径OC=1,OC⊥PC,
∵∠AOB=45°,OA∥PC,
∴∠OPC=45°,
∴PC=OC=1,
∴OP=
,
同理,原点左侧的距离也是
所以x的取值范围是0<x≤
故选A.
 解:设切点为C,连接OC,则
解:设切点为C,连接OC,则圆的半径OC=1,OC⊥PC,
∵∠AOB=45°,OA∥PC,
∴∠OPC=45°,
∴PC=OC=1,
∴OP=
| 2 |
同理,原点左侧的距离也是
| 2 |
所以x的取值范围是0<x≤
| 2 |
故选A.
点评:此题注意求出相切的时候的X值,即可分析出X的取值范围.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 24、如图,直线CD经过线段AB的一个端点B,∠ABC=50°,点P为直线CD上一点;已知△PAB是以AB为底边的等腰三角形,⊙O是以AB为直径的圆.
24、如图,直线CD经过线段AB的一个端点B,∠ABC=50°,点P为直线CD上一点;已知△PAB是以AB为底边的等腰三角形,⊙O是以AB为直径的圆. 如图,已知⊙O是以数轴原点O为原点,半径为2的圆,∠AOB=60°,点P是在数轴上运动的动点,若过P且与OA平行(或重合)的直线l与⊙O有公共点,求动点P所表示的数的取值范围.
如图,已知⊙O是以数轴原点O为原点,半径为2的圆,∠AOB=60°,点P是在数轴上运动的动点,若过P且与OA平行(或重合)的直线l与⊙O有公共点,求动点P所表示的数的取值范围. 如图,已知A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12.
如图,已知A、B、C是数轴上三点,点C表示的数为6,BC=4,AB=12. 如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)
如图,已知A,B两点在数轴上,点A表示的数为-10,OB=3OA,点M以每秒3个单位长度的速度从点A向右运动.点N以每秒2个单位长度的速度从点O向右运动(点M、点N同时出发)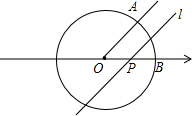 如图,已知⊙O是以数轴原点O为原点,半径为2的圆,∠AOB=60°,点P是在数轴上运动的动点,若过P且与OA平行(或重合)的直线l与⊙O有公共点,求动点P所表示的数的取值范围.
如图,已知⊙O是以数轴原点O为原点,半径为2的圆,∠AOB=60°,点P是在数轴上运动的动点,若过P且与OA平行(或重合)的直线l与⊙O有公共点,求动点P所表示的数的取值范围.