题目内容
如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心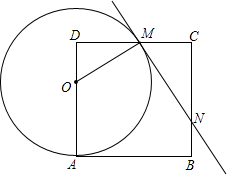 ,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.(1)求证:△ODM∽△MCN;
(2)设DM=x,求OA的长(用含x的代数式表示);
(3)在点O的运动过程中,设△CMN的周长为P,试用含x的代数式表示P,你能发现怎样的结论?
分析:(1)依题意可得∠OMC=∠MNC,然后可证得△ODM∽△MCN.
(2)设DM=x,OA=OM=R,OD=AD-OA=8-R,根据勾股定理求出OA的值.
(3)由1可求证△ODM∽△MCN,利用线段比求出CN,MN的值.然后可求出△CMN的周长等于CM+CN+MN,把各个线段消去代入可求出周长.
(2)设DM=x,OA=OM=R,OD=AD-OA=8-R,根据勾股定理求出OA的值.
(3)由1可求证△ODM∽△MCN,利用线段比求出CN,MN的值.然后可求出△CMN的周长等于CM+CN+MN,把各个线段消去代入可求出周长.
解答:(1)证明:∵MN切⊙O于点M,
∴∠OMN=90°;(1分)
∵∠OMD+∠CMN=90°,∠CMN+∠CNM=90°;
∴∠OMD=∠MNC;(2分)
又∵∠D=∠C=90°;
∴△ODM∽△MCN,(3分)
(2)解:在Rt△ODM中,DM=x,设OA=OM=R;
∴OD=AD-OA=8-R,(4分)
由勾股定理得:(8-R)2+x2=R2,(5分)
∴64-16R+R2+x2=R2,
∴OA=R=
(0<x<8);(6分)
(3)解法一:∵CM=CD-DM=8-x,
又∵OD=8-R=8-
=
,
且有△ODM∽△MCN,
∴
=
,
∴代入得到CN=
;(7分)
同理
=
,
∴代入得到MN=
;(8分)
∴△CMN的周长为P=CM+CN+MN=(8-x)+
+
=(8-x)+(x+8)=16.(9分)
发现:在点O的运动过程中,△CMN的周长P始终为16,是一个定值.(10分)
解法二:在Rt△ODM中,OD=8-R=8-
=
,
设△ODM的周长P′=OD+DM+OM=
+x+
=x+8;(7分)
而△MCN∽△ODM,且相似比k=
=(8-x)•
=
;(8分)
∵
=
,
∴△MCN的周长为P=(x+8)•
=16.(9分)
发现:在点O的运动过程中,△CMN的周长P始终为16,是一个定值.(10分)
∴∠OMN=90°;(1分)
∵∠OMD+∠CMN=90°,∠CMN+∠CNM=90°;
∴∠OMD=∠MNC;(2分)
又∵∠D=∠C=90°;
∴△ODM∽△MCN,(3分)
(2)解:在Rt△ODM中,DM=x,设OA=OM=R;
∴OD=AD-OA=8-R,(4分)
由勾股定理得:(8-R)2+x2=R2,(5分)
∴64-16R+R2+x2=R2,
∴OA=R=
| x2+64 |
| 16 |
(3)解法一:∵CM=CD-DM=8-x,
又∵OD=8-R=8-
| x2+64 |
| 16 |
| 64-x2 |
| 16 |
且有△ODM∽△MCN,
∴
| MC |
| OD |
| CN |
| DM |
∴代入得到CN=
| 16x |
| x+8 |
同理
| MC |
| OD |
| MN |
| OM |
∴代入得到MN=
| x2+64 |
| x+8 |
∴△CMN的周长为P=CM+CN+MN=(8-x)+
| 16x |
| x+8 |
| x2+64 |
| x+8 |
发现:在点O的运动过程中,△CMN的周长P始终为16,是一个定值.(10分)
解法二:在Rt△ODM中,OD=8-R=8-
| x2+64 |
| 16 |
| 64-x2 |
| 16 |
设△ODM的周长P′=OD+DM+OM=
| 64-x2 |
| 16 |
| x2+64 |
| 16 |
而△MCN∽△ODM,且相似比k=
| CM |
| OD |
| 16 |
| 64-x2 |
| 16 |
| 8+x |
∵
| △MCN的周长P |
| △ODM的周长P′ |
| 16 |
| 8+x |
∴△MCN的周长为P=(x+8)•
| 16 |
| x+8 |
发现:在点O的运动过程中,△CMN的周长P始终为16,是一个定值.(10分)
点评:本题考查的是相似三角形的判定,正方形的判定,勾股定理、切线性质和二次函数的综合运用等有关知识.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案 培优三好生系列答案
培优三好生系列答案
相关题目
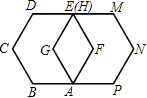 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.