题目内容
【题目】(1)问题发现
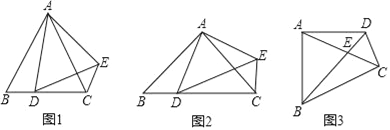
如图1,△ABC和△ADE均为等边三角形,点D在边BC上,连接CE.请填空:
①∠ACE的度数为 ;
②线段AC、CD、CE之间的数量关系为 .
(2)拓展探究
如图2,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,点D在边BC上,连接CE.请判断∠ACE的度数及线段AC、CD、CE之间的数量关系,并说明理由.
(3)解决问题
如图3,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD=2,CD=1,AC与BD交于点E,请直接写出线段AC的长度.
【答案】(1)①60°;②AC=CD+CE;(2)∠ACE=45°,![]() AC=CD+CE(3)
AC=CD+CE(3)![]()
【解析】试题分析:(1)、根据等边三角形的性质得出∠BAD=∠CAE,从而得出△BAD和△CAE全等,从而得出∠ACE=∠B=60°,根据全等得出BD=CE,从而得出AC=CD+CE;(2)、根据第一题同样的方法得出△BAD和△CAE全等,从而得出BC=CD+CE,然后根据等腰直角三角形的性质得出BC=![]() AC,从而得出答案;(3)、过A作AC的垂线,交CB的延长线于点F,根据题意得出A、B、C、D四点共圆,即∠ADB=∠ACB=45°,根据第二步的结论AC=
AC,从而得出答案;(3)、过A作AC的垂线,交CB的延长线于点F,根据题意得出A、B、C、D四点共圆,即∠ADB=∠ACB=45°,根据第二步的结论AC=![]() 得出答案.
得出答案.
试题解析:(1)①∵△ABC和△ADE均为等边三角形,∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=60°,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC, 即∠BAD=∠CAE, ∴△BAD≌△CAE(SAS),
∴∠ACE=∠B=60°,
②线段AC、CD、CE之间的数量关系为:AC=CD+CE;
理由是:由①得:△BAD≌△CAE, ∴BD=CE, ∵AC=BC=BD+CD, ∴AC=CD+CE;
(2)∠ACE=45°,![]() AC=CD+CE,理由是:
AC=CD+CE,理由是:
如图2,∵△ABC和△ADE均为等腰直角三角形,且∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠BAC﹣∠DAC=∠DAE﹣∠DAC, 即∠BAD=∠CAE, ∴△ABD≌△ACE,
∴BD=CE,∠ACE=∠B=45°, ∵BC=CD+BD, ∴BC=CD+CE,
∵在等腰直角三角形ABC中,BC=![]() AC, ∴
AC, ∴![]() AC=CD+CE;
AC=CD+CE;
(3)如图3,过A作AC的垂线,交CB的延长线于点F,
∵∠BAD=∠BCD=90°,AB=AD=2,CD=1, ∴BD=2![]() ,BC=
,BC=![]() , ∵∠BAD=∠BCD=90°,
, ∵∠BAD=∠BCD=90°,
∴∠BAD+∠BCD=180°, ∴A、B、C、D四点共圆, ∴∠ADB=∠ACB=45°,
∴△ACF是等腰直角三角形, 由(2)得:![]() AC=BC+CD, ∴AC=
AC=BC+CD, ∴AC=![]() =
=![]() =
=![]() .
.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案