题目内容
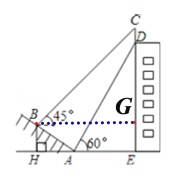
【题目】(本题满分10分)如图,某大楼的顶部竖有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度![]() ,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据: ![]() ,
, ![]() )
)
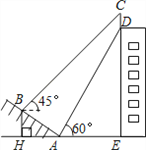
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
【答案】(1)5;(2)2.7米
【解析】试题分析:(1)在Rt△ABF中,先由坡度![]() ,可求出∠BAH=30°,从而根据30°角的性质求出BH的长;
,可求出∠BAH=30°,从而根据30°角的性质求出BH的长;
(2)在Rt△ABF中,由勾股定理求出AH的长,从而可求出BG的长度;在Rt△BGC中,可求出CG=BG=5![]() +15;在Rt△ADE中,求出DE=15
+15;在Rt△ADE中,求出DE=15![]() ;最后根据CD=CG+GE﹣DE求解即可.
;最后根据CD=CG+GE﹣DE求解即可.
解:(1)Rt△ABF中,
i=tan∠BAH=![]() ,
,
∴∠BAH=30°,
∴BH=![]() AB=5;
AB=5;
(2)过B作BG⊥DE于G,
由(1)得:BH=5,AH=5![]() ,
,
∴BG=AH+AE=5![]() +15,
+15,
Rt△BGC中,∠CBG=45°,
∴CG=BG=5![]() +15.
+15.
Rt△ADE中,∠DAE=60°,AE=15,
∴DE=![]() AE=15
AE=15![]() .
.
∴CD=CG+GE﹣DE=5![]() +15+5﹣15
+15+5﹣15![]() =20﹣10
=20﹣10![]() ≈2.7m.
≈2.7m.
答:宣传牌CD高约2.7米.

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】一辆小汽车在高速公路上从静止到起动10秒内的速度经测量如下表:
时间(秒) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
速度(米/秒) | 0 | 0.3 | 1.3 | 2.8 | 4.9 | 7.6 | 11.0 | 14.1 | 18.4 | 24.2 | 28.9 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用T表示时间,V表示速度,那么随着T的变化,V的变化趋势是什么?
(3)当T每增加1秒,V的变化情况相同吗?在哪1秒钟,V的增加最大?
(4)若高速公路上小汽车行驶速度的上限为120千米/小时,试估计大约还需几秒这辆小汽车的速度就将达到这个上限。