题目内容
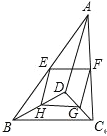
【题目】在△AFD和△BEC中，点A、E、F、C在同一直线上，有下面四个论断：(1)AD=CB；(2)AE=CF；(3)∠B=∠D；(4)AD∥BC．请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出证明过程．
【答案】详见解析，（答案不唯一，正确即可）
【解析】试题分析：选择（A）（B）（D）得到（C），组成命题为如果AD=CB，AE=CF，AD∥BC，那么∠B=∠D；利用“SAS”证明△ADF≌△CBE，然后根据相似的性质得到∠D=∠B．（答案不唯一，正确即可）
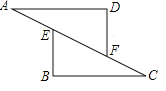
试题解析：解：如果AD=CB，AE=CF，AD∥BC，那么∠B=∠D．
证明如下：∵AD∥BC，
∴∠A=∠C，
∵AE=CF，
∴AE+EF=EF+CF，
∴AF=CE，
在△ADF和△CBE中，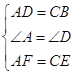
，
∴△ADF≌△CBE（SAS），
∴∠D=∠B．
练习册系列答案
相关题目
【题目】某市某一周的PM2.5（大气中直径小于等于2.5微米的颗粒物，也称可入肺颗粒物指数如表，则该周PM2.5指数的众数和中位数分别是________
PM2.5指数 | 150 | 155 | 160 | 165 |
天 数 | 3 | 2 | 1 | 1 |
