题目内容
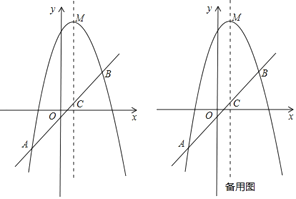
【题目】已知，抛物线与x轴交于A、B两点(点A在点B的左侧)，且AB=4，顶点P(3，-4)．
（1）求抛物线的解析式；
（2）若点M在抛物线上，且△MAB的面积为24，求M点的坐标．
【答案】（1）y=x2-6x+5；（2）M1(-1，12)，M2(7，12)
【解析】
（1）先求出抛物线的对称轴，从而求出点A和点B的坐标，设抛物线的解析式为：y=a(x-3)2-4，将点B的坐标代入即可求出结论；
（2）设点M(m，m2-6m+5)，根据三角形的面积公式可得
AB|m2-6m+5|=24，解一元二次方程即可求出结论．
解：（1）∵抛物线的顶点P(3，-4)，
∴抛物线的对称轴为直线x=3．
又在x轴上所截得的线段AB的长为4，
∴点A、B到对称轴的距离为2．
∴点A的坐标为(1，0)，点B的坐标为(5，0)．
设抛物线的解析式为：y=a(x-3)2-4．
将点B(5，0)代入可得:0=a(5-3)2-4．
解得a=1．
故抛物线的解析式为：y=(x-3)2-4，即y=x2-6x+5．
（2）设点M(m，m2-6m+5)，
∵S△MAB=24，
∴AB|m2-6m+5|=24，即m2-6m+5=±12．
∴m2-6m+5=12或m2-6m+5=-12．
由m2-6m+5=12得m2-6m-7=0．
解得：x1=-1，x2=7，
∴M1(-1，12)，M2(7，12)；
由m2-6m+5=-12得m2-6m+17=0．
=(-6)2-4×17=-32＜0．
∴方程无解，舍去．
综上：M1(-1，12)，M2(7，12)．
练习册系列答案
名校课堂系列答案
相关题目
