题目内容
【题目】如图,四边形ABCD是边长为2,一个锐角等于60°的菱形纸片,小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合,按顺时针方向旋转三角形纸片,使它的两边分别交CB、BA(或它们的延长线)于点E、F,∠EDF=60°,当CE=AF时,如图1小芳同学得出的结论是DE=DF.
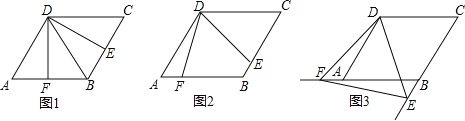
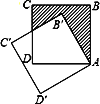
(1)继续旋转三角形纸片,当CE≠AF时,如图2小芳的结论是否成立?若成立,加以证明;若不成立,请说明理由;
(2)再次旋转三角形纸片,当点E、F分别在CB、BA的延长线上时,如图3请直接写出DE与DF的数量关系;
(3)连EF,若△DEF的面积为y,CE=x,求y与x的关系式,并指出当x为何值时,y有最小值,最小值是多少?
【答案】(1)成立,证明见解析;(2)DF=DE.(3)当x=0时,y最小值=![]() .
.
【解析】
试题分析:(1)如图1,连接BD.根据题干条件首先证明∠ADF=∠BDE,然后证明△ADF≌△BDE(ASA),得DF=DE;
(2)如图2,连接BD.根据题干条件首先证明∠ADF=∠BDE,然后证明△ADF≌△BDE(ASA),得DF=DE;
(3)根据(2)中的△ADF≌△BDE得到:S△ADF=S△BDE,AF=BE.所以△DEF的面积转化为:y=S△BEF+S△ABD.据此列出y关于x的二次函数,通过求二次函数的最值来求y的最小值.
试题解析:(1)DF=DE.理由如下:
如图1,连接BD.
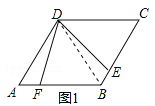
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.∵在△ADF与△BDE中,
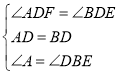 ,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(2)DF=DE.理由如下:
如图2,连接BD.
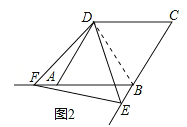
∵四边形ABCD是菱形,
∴AD=AB.
又∵∠A=60°,
∴△ABD是等边三角形,
∴AD=BD,∠ADB=60°,
∴∠DBE=∠A=60°
∵∠EDF=60°,
∴∠ADF=∠BDE.
∵在△ADF与△BDE中,
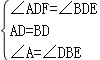 ,
,
∴△ADF≌△BDE(ASA),
∴DF=DE;
(3)由(2)知,△ADF≌△BDE.则S△ADF=S△BDE,AF=BE=x.
依题意得:y=S△BEF+S△ABD=![]() (2+x)xsin60°+
(2+x)xsin60°+![]() ×2×2sin60°=
×2×2sin60°=![]() (x+1)2+
(x+1)2+![]() .
.
即y=![]() (x+1)2+
(x+1)2+![]() .
.
∵![]() >0,
>0,
∴该抛物线的开口方向向上,
∴当x=0即点E、B重合时,y最小值=![]() .
.

 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案