题目内容
若把直角三角形的三边都增加同样的长度,则新三角形是
- A.锐角三角形
- B.直角三角形
- C.钝角三角形
- D.不能确定
A
分析:先设出原来的三边为a、b、c且c2=a2+b2,以及增加同样的长度为x,得到新的三角形的三边为a+x、b+x、c+x,知c+x为最大边,所以所对的角最大,然后根据余弦定理判断出余弦值为正数,所以最大角为锐角,得到三角形为锐角三角形.
解答:设增加同样的长度为x,原三边长为a、b、c,且c2=a2+b2,c为最大边;
新的三角形的三边长为a+x、b+x、c+x,知c+x为最大边,其对应角最大.
而(a+x)2+(b+x)2-(c+x)2=x2+2(a+b-c)x>0,
由余弦定理知新的三角形的最大角的余弦=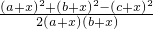 >0,则为锐角,
>0,则为锐角,
那么它为锐角三角形.
另法:设增加同样的长度为x,原三边长为a、b、c,且c2=a2+b2,c为最大边;
新的三角形的三边长为a+x、b+x、c+x,知c+x为最大边,其对应角最大.
而(a+x)2+(b+x)2-(c+x)2=x2+2(a+b-c)x>0,
∴(a+x)2+(b+x)2>(c+x)2,
∴新三角形为锐角三角形,
故选A.
点评:本题考查的是勾股定理及余弦定理的应用,再解答此题时要注意先设出原三边长为a、b、c,且c2=a2+b2,c为最大边,再根据余弦定理进行解答.
分析:先设出原来的三边为a、b、c且c2=a2+b2,以及增加同样的长度为x,得到新的三角形的三边为a+x、b+x、c+x,知c+x为最大边,所以所对的角最大,然后根据余弦定理判断出余弦值为正数,所以最大角为锐角,得到三角形为锐角三角形.
解答:设增加同样的长度为x,原三边长为a、b、c,且c2=a2+b2,c为最大边;
新的三角形的三边长为a+x、b+x、c+x,知c+x为最大边,其对应角最大.
而(a+x)2+(b+x)2-(c+x)2=x2+2(a+b-c)x>0,
由余弦定理知新的三角形的最大角的余弦=
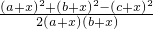 >0,则为锐角,
>0,则为锐角,那么它为锐角三角形.
另法:设增加同样的长度为x,原三边长为a、b、c,且c2=a2+b2,c为最大边;
新的三角形的三边长为a+x、b+x、c+x,知c+x为最大边,其对应角最大.
而(a+x)2+(b+x)2-(c+x)2=x2+2(a+b-c)x>0,
∴(a+x)2+(b+x)2>(c+x)2,
∴新三角形为锐角三角形,
故选A.
点评:本题考查的是勾股定理及余弦定理的应用,再解答此题时要注意先设出原三边长为a、b、c,且c2=a2+b2,c为最大边,再根据余弦定理进行解答.

练习册系列答案
相关题目
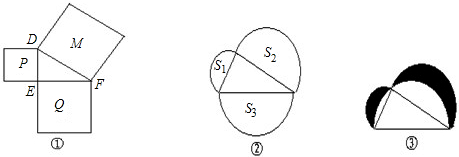 (一)小明在玩积木游戏时,把三个正方形积木摆成一定的形状,正视图如图①,
(一)小明在玩积木游戏时,把三个正方形积木摆成一定的形状,正视图如图①,
