题目内容
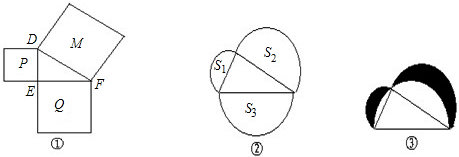
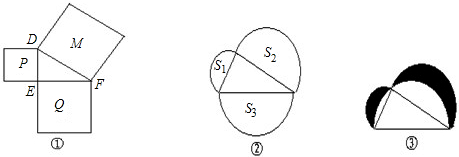 (一)小明在玩积木游戏时,把三个正方形积木摆成一定的形状,正视图如图①,
(一)小明在玩积木游戏时,把三个正方形积木摆成一定的形状,正视图如图①,问题(1):若此中的三角形△DEF为直角三角形,P的面积为9,Q的面积为15,则M的面积为
问题(2):若P的面积为36cm2,Q的面积为64 cm2,同时M的面积为100 cm2,则△DEF为
(二)图形变化:
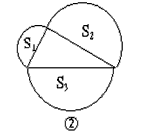
Ⅰ如图②,分别以直角三角形的三边为直径向三角形外作三个半圆,你能找出这三个半圆的面积之间有什么关系吗?请说明理由.
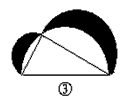
Ⅱ如图③,如果直角三角形两直角边的长分别为3和4,以直角三角形的三边为直径作半圆,你能利用上面中的结论求出阴影部分的面积吗?
分析:(一)(1)根据正方形的面积公式结合勾股定理就可发现大正方形的面积是两个小正方形的面积和;
(2)根据大正方形的面积等于两个小正方形的面积和,可以得到其中两条边平方的和等于第三条边的平方,即根据勾股定理的逆定理就可证明是直角三角形.
(二)I根据半圆的面积公式以及勾股定理就可发现:两个小半圆的面积和等于大半圆的面积.
II根据上述结论就可发现:阴影部分的面积=直角三角形的面积.
(2)根据大正方形的面积等于两个小正方形的面积和,可以得到其中两条边平方的和等于第三条边的平方,即根据勾股定理的逆定理就可证明是直角三角形.
(二)I根据半圆的面积公式以及勾股定理就可发现:两个小半圆的面积和等于大半圆的面积.
II根据上述结论就可发现:阴影部分的面积=直角三角形的面积.
解答:解:(一)∵P=DE2,Q=EF2,M=DF2,DE2+EF2=DF2,
∴M=P+Q=24;
∵M=P+Q,
即DE2+EF2=DF2,
∴△DEF是直角三角形;
故答案为:24;直角,
(二)I设直角三角形的边从小到大分别是a,b,c.则a2+b2=c2.
两边同除以
,即得:两小半圆的面积和等于大半圆的面积.
II根据I中的结论,得阴影部分的面积=S直角三角形的面积=
×3×4=6.
∴M=P+Q=24;
∵M=P+Q,
即DE2+EF2=DF2,
∴△DEF是直角三角形;
故答案为:24;直角,
(二)I设直角三角形的边从小到大分别是a,b,c.则a2+b2=c2.
两边同除以
| π |
| 8 |
II根据I中的结论,得阴影部分的面积=S直角三角形的面积=
| 1 |
| 2 |
点评:注意:分别以直角三角形的边作相同的图形,则两个小图形的面积等于大图形的面积.

练习册系列答案
相关题目
 探究题
探究题 (一)小明在玩积木游戏时,把三个正方形积木摆成一定的形状,正视图如图①,
(一)小明在玩积木游戏时,把三个正方形积木摆成一定的形状,正视图如图①,