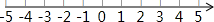题目内容
(1)求不等式组
|
(2)解方程
| 1 |
| 2x-4 |
| 1 |
| 2 |
| 3 |
| 2-x |
(3)化简:(
| x+2 |
| x2-2x |
| x-1 |
| x2-4x+4 |
| x-4 |
| x |
分析:(1)先求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其整数解即可,
(2)观察可得最简公分母是(2x-4),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(3)先化简,再将1代入即可.
(2)观察可得最简公分母是(2x-4),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
(3)先化简,再将1代入即可.
解答:解:(1)
,
解①得,x<2;
解②得,x≥-
;
∴不等式组的解集为-
≤x<2,
∴不等式组的整数解为-1,0,1;
(2)方程的两边同乘(2x-4),得
1+x-2=-6,
解得x=-5.
检验:把x=-5代入(2x-4)=-14≠0.
∴原方程的解为:x=-14.
(3)原式=
×
=
,
∵x≠0,2,4,
∴x=1,
∴原式=
=1.
|
解①得,x<2;
解②得,x≥-
| 7 |
| 4 |
∴不等式组的解集为-
| 7 |
| 4 |
∴不等式组的整数解为-1,0,1;
(2)方程的两边同乘(2x-4),得
1+x-2=-6,
解得x=-5.
检验:把x=-5代入(2x-4)=-14≠0.
∴原方程的解为:x=-14.
(3)原式=
| (x+2)(x-2)-x(x-1) |
| x(x-2)2 |
| x |
| x-4 |
=
| 1 |
| (x-2)2 |
∵x≠0,2,4,
∴x=1,
∴原式=
| 1 |
| (1-2)2 |
点评:本题主要考查了解不等式组、解分式方程,注:(1)解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.
(2)解分式方程一定注意要验根.
(2)解分式方程一定注意要验根.

练习册系列答案
相关题目