题目内容
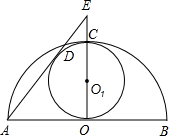如图，AB是半圆⊙O的直径，半径OC⊥AB，⊙O的直径是OC，AD切⊙O1于D，交OC的延长线于E，设⊙O1的半径为r，那么用含r的代数式表示DE，结果是DE=分析：连接O1D，得∠O1DE=90°，是运用切线性质常用的作辅助线方法，构造三角形相似，得出相似比，结合直角三角形的勾股定理解题．
解答：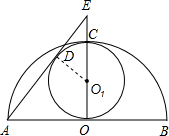
解：连接O1D，可得到∠O1DE=∠AOE=90°，∠E=∠E，
∴△O1DE∽△AOE，
则DE：OE=O1D：OA=1：2；
设DE=x，则OE=2x，O1E=2x-r，
由O1E2-O1D2=DE2，得（2x-r）2-r2=x2，
解得x=0（舍去）或x=
r，即DE=
r．
解：连接O1D，可得到∠O1DE=∠AOE=90°，∠E=∠E，∴△O1DE∽△AOE，
则DE：OE=O1D：OA=1：2；
设DE=x，则OE=2x，O1E=2x-r，
由O1E2-O1D2=DE2，得（2x-r）2-r2=x2，
解得x=0（舍去）或x=
| 4 |
| 3 |
| 4 |
| 3 |
点评：解决本题的关键是利用相似求出所求线段所在的直角三角形中其他线段的长度．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，AB是半圆O的直径，∠BAC=30°，BC为半圆的切线，切点为B，且BC=4\sqrt{3}．
如图，AB是半圆O的直径，AC=AD，OC=2，∠CAB=30°，则点O到CD的距离OE=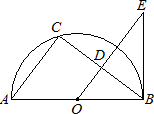
AC交BC于点D，在OD的延长线上取一点E，连接EB，使∠OEB=∠ABC．
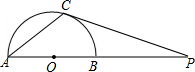（2013•镇江）如图，AB是半圆O的直径，点P在AB的延长线上，PC切半圆O于点C，连接AC．若∠CPA=20°，则∠A=