题目内容
【题目】在学习了一次函数图像后,张明、李丽和王林三位同学在赵老师的指导下,对一次函数
进行了探究学习,请根据他们的对话解答问题.
(1)张明:当
时,我能求出直线与
轴的交点坐标为 ;
李丽:当
时,我能求出直线与坐标轴围成的三角形的面积为 ;
(2)王林:根据你们的探究,我发现无论
取何值,直线总是经过一个固定的点,请求出这个定点的坐标.
(3)赵老师:我来考考你们,如果点
的坐标为
,该点到直线的距离存在最大值吗?若存在,试求出该最大值;若不存在,请说明理由.
【答案】(1) （3,0）， 
； (2) （2,1）； (3) 
；
【解析】
(1) 张明：将k值代入求出解析式即可得到答案；
李丽: 将k值代入求出解析式，得到直线与x轴和y轴的交点，即可得到答案；
(2) 将
转化为（y-1）=k（x-2）正比例函数，即可求出；
(3) 由图像 必过（2,1）设必过点为A,P到直线的距离为PB，发现直角三角形ABP中PA是最大值，所以当PA与垂直时最大，求出即可.
解：(1)张明： 将
代入
得到y=-x-2×（-1）+1
y=-x+3
令y=0 得-x+3=0，得x=3
所以直线与
轴的交点坐标为（3,0）
李丽：将
代入
得到 y=2x-3
直线与x轴的交点为（
，0） 直线与y轴的交点为（0，-3）
所以直线与坐标轴围成的三角形的面积=
(2) ∵转化为（y-1）=k（x-2）正比例函数
∴（y-1）=k（x-2）必过（0,0）
∴此时x=2，y=1
通过图像平移得到必过（2,1）
(3)
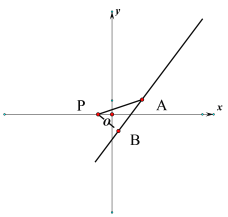
由图像 必过（2,1）
设必过点为A,P到直线的距离为PB
由图中可以得到直角三角形ABP中AP大于直角边PB
所以P到最大距离为PA与直线垂直，即为PA
∵ P（-1,0）A（2,1）
得到PA=
答：点P到最大距离的距离存在最大值为.
