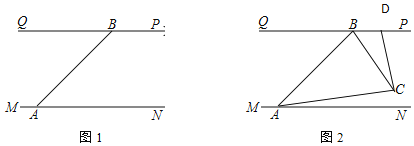题目内容
【题目】①如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD,BD,BC,AC的中点.
(1)求证:四边形EFGH是平行四边形;
(2)当四边形ABCD满足一个什么条件时,四边形EFGH是菱形?并证明你的结论;
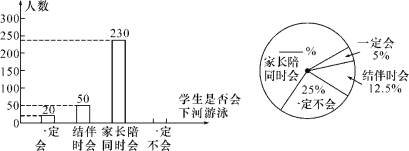
②如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC中点,CE⊥AD于E,BF∥AC,交CE的延长线与点F.求证:AB垂直平分DF.
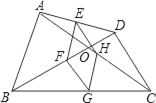
【答案】①(1)见解析;(2)见解析; ②见解析.
【解析】
①(1)由三角形中位线知识可得EF=GH,EF∥GH,继而可得四边形EFGH是平行四边形;
(2)要是菱形,只需增加相邻两边相等,如要得到EF=GF,由中位线知识,只须AB=CD.
②由FB∥AC,∠ACB=90°可得∠FBC=90°,继而可得∠DBA=45°,通过证明Rt△ADC≌Rt△FBC,可得DB=FB,继而可证得答案.
①(1)∵E、F分别是AD、BD中点,
∴EF∥AB,EF=![]() AB,
AB,
同理GH∥AB,GH=![]() AB,
AB,
∴EF=GH,EF∥GH,
∴四边形EFGH是平行四边形;
(2)当四边形ABCD满足AB=CD时,四边形EFGH是菱形,证明如下:
∵F、G分别是BD、BC中点,∴GF=![]() CD,
CD,
∵AB=CD,∴EF=GF,
又∵四边形EFGH是平行四边形,
∴四边形EFGH是菱形;

②∵∠ACB=90°,Rt△ADC中,∠1+∠2=90°,
∵AD⊥CF,在Rt△EDC中,∠3+∠2=90°,得:∠1=∠3,
∵FB∥AC,∠ACB=90°,∴∠FBC=90°,得:△FBC是直角三角形,
∵AC=BC,∠1=∠3,△FBC是直角三角形,
∴Rt△ADC≌Rt△FBC,
∴CD=FB,∵CD=DB,∴DB=FB,
∵AC=BC、∠ACB=90°,∴∠4=45°,∴AB是∠CBF平分线,
所以,AB垂直平分DF(等腰三角形中的三线合一定理).