Question

如图，已知OE平分∠AOC，OF平分∠BOC  (12分)

（1）若∠AOB是直角，∠BOC=60°，求∠EOF的度数。
（2）若∠AOC=x°，∠EOF=y°，∠BOC=60°，请用x 的代数式来表示y．
（3）如果∠AOC+∠EOF=210°，∠BOC=60°，则∠EOF是多少度？

Answer 1

（1） 45°（2）y=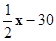（3）50

试题考查知识点：角的平分线的性质，函数关系式的建立
思路分析：利用角的平分线的性质进行推算
具体解答过程：
∵OE平分∠AOC，OF平分∠BOC
∴∠AOE=∠COE=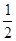∠AOC，∠BOF=∠COF=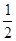∠BOC
（1）如果∠AOB是直角，∠BOC=60°，如图所示
∵∠AOC=∠AOB+∠BOC=90°+60°=150°
∴∠COE=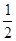∠AOC=75°
∵∠COF=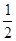∠BOC=30°
∴∠EOF=∠COE-∠COF=75°-30°=45°
（2）若∠AOC=x°，∠EOF=y°，∠BOC=60°
∵∠COE=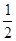∠AOC=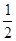x°，∠COF=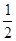∠BOC=30°
∴∠EOF=∠COE-∠COF=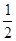x°-30°即y=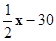
（3）由（2）已得，∠EOF=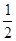x°-30°其中，∠AOC=x°
∵∠AOC+∠EOF=210°，∠BOC=60°
∴x°+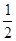（x°-30°）=210°即x=80，∠AOC=160°
∴∠EOF=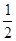x°-30°=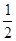×160°-30°=50°
试题点评：这道题目中的三问依次是递进的关系，注意前者在后者中利用，可以大大提高效率。