Question

（2006•襄阳）如图1所示，把一张矩形纸片ABCD沿对角线BD折叠，将重合部分△BFD剪去，得到△ABF和△EDF．
（1）判断△ABF与△EDF是否全等并加以证明；

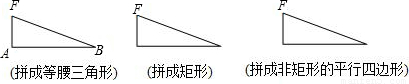
（2）把△ABF与△EDF不重合地拼在一起，可拼成特殊三角形和特殊四边形，在图2中，按要求将拼图补画完整．要求：①任选一图用尺规作图，保留作图痕迹；②其余两图画图工具不限．

Answer 1

【答案】分析：①由折叠的性质求证△ABF≌△EFD；
②拼成等腰三角形的作法：以点A为圆心，AF的长为半径画弧，以点B为圆心，BF的长为半径画弧，与前弧交于点G，连接AG，BG，则△ABG是所求的三角形．
解答：解：（1）全等
证明：由折叠的性质知，ED=CD=AB，
又∵∠E=∠A=90°，∠EFD=∠AFB，
∴△ABF≌△EFD；

解：（2）


点评：本题考查了折叠的性质，全等三角形的判定，作三角形与已知三角形全等．