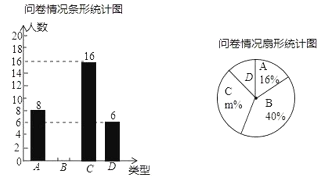
题目内容
【题目】已知有理数a、b、c满足：a+c＜0，ac＞0，|b|＝b，
（1）比较大小：a______0；b_____；c_____0；
（2）先去绝对值，再化简：|a﹣2b+c|﹣
+2|b﹣2c|的值．
【答案】（1）＜；≥；＜；（2）4b﹣3c．
【解析】
（1）通过加法、乘法的符号法则，判断a、b的正负，通过绝对值的意义，判断b的正负；
（2）根据加法的符号法则，先判断a﹣2b+c、2a+4c、b﹣2c的正负，再根绝绝对值的意义化去绝对值后再计算．
解：（1）因为a+c＜0，ac＞0，|b|＝b，
所以a＜0，c＜0，b≥0．
故答案为：＜；≥；＜
（2）∵a＜0，c＜0，b≥0．
∴a﹣2b+c＜0，2a+4c＜0，b﹣2c＞0，
∴原式＝﹣（a﹣2b+c）﹣
+2（b﹣2c）
＝﹣a+2b﹣c+a+2c+2b﹣4c
＝4b﹣3c．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
