题目内容
已知,边长为5的正方形ABCO在如图所示的直角坐标系中,点M(t,0)为x轴上一动点,过A作直线MC的垂线交y轴于点N.(1)当t=2时,求直线MC的解析式;
(2)设△AMN的面积为S,当S=3时,求t的值;
(3)取点P(1,y),如果存在以M、N、C、P为顶点的四边形是等腰梯形,当t<0时,甲同学说:y与t应同时满足方程t2-yt-5=0和y2-2t2-10y+26=0;乙同学说:y与t应同时满足方程t2-yt-5=0和y2+8t-24=0,你认为谁的说法正确,并说明理由.再直接写出t>0时满足题意的一个点P的坐标.
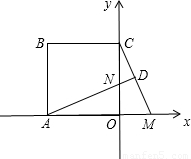
【答案】分析:(1)根据边长为5的正方形ABCO在如图所示的直角坐标系中,和点M(t,0)为x轴上一动点,分别求出k和b的值即可.
(2)分别根据t>0,-5<t<0,t<-5时,用t表示出△AMN的面积,解一元二次方程即可求出;
(3)作PH⊥y轴,则△PHN∽△MOC,由Rt△PCH得1+(y-5)2=2t2,可证甲正确;
由直线x=1与x轴交于E,由Rt△PME得,(5-t)2=y2+(1-t)2,可证乙正确.
解答: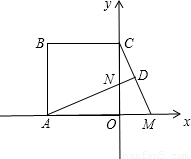 解:(1)∵边长为5的正方形ABCO在如图所示的直角坐标系中,
解:(1)∵边长为5的正方形ABCO在如图所示的直角坐标系中,
∴将x=0,y=5代入y=kx+b,解得b=5
∵点M(t,0)为x轴上一动点,过A作直线MC的垂线交y轴于点N,
∴将x=2,y=0代入y=kx+b,解得k=- .
.
∴当t=2时,直线MC的解析式为: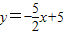 ;
;
(2)CM斜率k=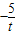 ,则AN斜率
,则AN斜率
设AD的解析式为:y= x+b,
x+b,
∵过A(-5,0),
∴b=t,
∴N(0,t)
∴S= t2+
t2+ t(t>0)t=1,
t(t>0)t=1,
S=- t2-
t2- t(-5<t<0)t=-2,t=-3,
t(-5<t<0)t=-2,t=-3,
S= t2+
t2+ t(t<-5)t=-6都正确;
t(t<-5)t=-6都正确;
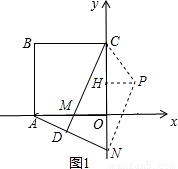
(3)作PH⊥y轴,如图1:
∵四边形NPMC是等腰梯形,
∴∠PNH=∠MCO,
∵∠PHN=∠MOC=90°,
∴△PHN∽△MOC,
得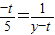 ,
,
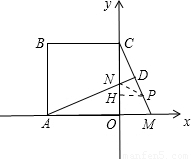 所以t2-yt-5=0,满足PN∥CM,
所以t2-yt-5=0,满足PN∥CM,
由Rt△PCH得1+(y-5)2=2t2,
所以y2-2t2-10y+26=0,满足PC=MN,故甲正确;
直线x=1与x轴交于E,由Rt△PME得,
(5-t)2=y2+(1-t)2
所以y2+8t-24=0,满足PM=CN,故乙正确;
P(1,6).
点评:此题涉及到的知识点较多,综合性强,通过此类题目的练习,利用学生系统的掌握所学知识,是一道很典型的题目.
(2)分别根据t>0,-5<t<0,t<-5时,用t表示出△AMN的面积,解一元二次方程即可求出;
(3)作PH⊥y轴,则△PHN∽△MOC,由Rt△PCH得1+(y-5)2=2t2,可证甲正确;
由直线x=1与x轴交于E,由Rt△PME得,(5-t)2=y2+(1-t)2,可证乙正确.
解答:
 解:(1)∵边长为5的正方形ABCO在如图所示的直角坐标系中,
解:(1)∵边长为5的正方形ABCO在如图所示的直角坐标系中,∴将x=0,y=5代入y=kx+b,解得b=5
∵点M(t,0)为x轴上一动点,过A作直线MC的垂线交y轴于点N,
∴将x=2,y=0代入y=kx+b,解得k=-
 .
.∴当t=2时,直线MC的解析式为:
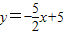 ;
;(2)CM斜率k=
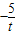 ,则AN斜率
,则AN斜率
设AD的解析式为:y=
 x+b,
x+b,∵过A(-5,0),
∴b=t,
∴N(0,t)
∴S=
 t2+
t2+ t(t>0)t=1,
t(t>0)t=1,S=-
 t2-
t2- t(-5<t<0)t=-2,t=-3,
t(-5<t<0)t=-2,t=-3,S=
 t2+
t2+ t(t<-5)t=-6都正确;
t(t<-5)t=-6都正确;
(3)作PH⊥y轴,如图1:
∵四边形NPMC是等腰梯形,
∴∠PNH=∠MCO,
∵∠PHN=∠MOC=90°,
∴△PHN∽△MOC,
得
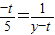 ,
, 所以t2-yt-5=0,满足PN∥CM,
所以t2-yt-5=0,满足PN∥CM,由Rt△PCH得1+(y-5)2=2t2,
所以y2-2t2-10y+26=0,满足PC=MN,故甲正确;
直线x=1与x轴交于E,由Rt△PME得,
(5-t)2=y2+(1-t)2
所以y2+8t-24=0,满足PM=CN,故乙正确;
P(1,6).
点评:此题涉及到的知识点较多,综合性强,通过此类题目的练习,利用学生系统的掌握所学知识,是一道很典型的题目.

练习册系列答案
相关题目
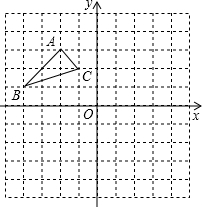
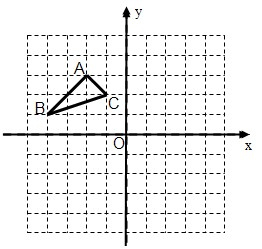 22、如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC;
22、如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC;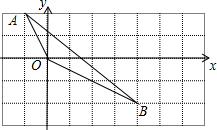 B先沿x轴正方向平移3个单位,再沿y轴负方向平移1个单位得到△A1O1B1.
B先沿x轴正方向平移3个单位,再沿y轴负方向平移1个单位得到△A1O1B1.

 如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC
如图:在平面直角坐标系中,网格中每一个小正方形的边长为1个单位长度;已知△ABC