题目内容
【题目】如图,在等腰直角△ABC中,∠ACB=90°,AC=BC= ![]()

(1)作⊙O,使它过点A、B、C(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)所作的圆中,圆心角∠BOC=°,圆的半径为 , 劣弧 ![]() 的长为 .
的长为 .
【答案】
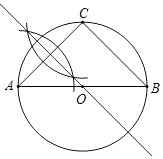
(1)解:如图所示,⊙O即为所求;
(2)解:90;1;![]() π
π
【解析】解:(2)如图所示,∠BOC=2∠A=90°, Rt△AOC中,AO=AC×cos∠A= ![]() ×
× ![]() =1,即圆的半径为1,
=1,即圆的半径为1,![]() =
= ![]() =
= ![]() π.
π.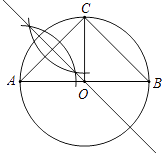
所以答案是:90,1, ![]() π.
π.
【考点精析】掌握等腰直角三角形和圆周角定理是解答本题的根本,需要知道等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目