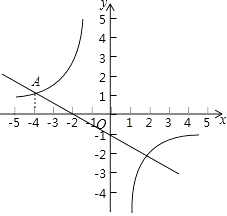题目内容
【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A、C在坐标轴上,点P在BC边上,直线l1:y=2x+3,直线l2:y=2x﹣3.
(1)分别求直线l1与x轴,直线l2与AB的交点坐标;
(2)已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;
(3)我们把直线l1和直线l2上的点所组成的图形为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且N点的横坐标为x,请直接写出x的取值范围(不用说明理由).
【答案】
(1)
解:直线l1:当y=0时,2x+3=0,x=﹣ ![]()
则直线l1与x轴坐标为(﹣ ![]() ,0)
,0)
直线l2:当y=3时,2x﹣3=3,x=3
则直线l2与AB的交点坐标为(3,3);
(2)
解:①若点A为直角顶点时,点M在第一象限,连结AC,
如图1,

∠APB>∠ACB>45°,
∴△APM不可能是等腰直角三角形,
∴点M不存在;
②若点P为直角顶点时,点M在第一象限,如图2,

过点M作MN⊥CB,交CB的延长线于点N,
则Rt△ABP≌Rt△PNM,
∴AB=PN=4,MN=BP,
设M(x,2x﹣3),则MN=x﹣4,
∴2x﹣3=4+3﹣(x﹣4),
x= ![]() ,
,
∴M( ![]() ,
, ![]() );
);
③若点M为直角顶点时,点M在第一象限,如图3,

设M1(x,2x﹣3),
过点M1作M1G1⊥OA,交BC于点H1,
则Rt△AM1G1≌Rt△PM1H1,
∴AG1=M1H1=3﹣(2x﹣3),
∴x+3﹣(2x﹣3)=4,
x=2
∴M1(2,1);
设M2(x,2x﹣3),
同理可得x+2x﹣3﹣3=4,
∴x= ![]() ,
,
∴M2( ![]() ,
, ![]() );
);
综上所述,点M的坐标为( ![]() ,
, ![]() ),(2,1),(
),(2,1),( ![]() ,
, ![]() );
);
(3)
解:x的取值范围为﹣ ![]() ≤x<0或0<x≤
≤x<0或0<x≤ ![]() 或
或 ![]() ≤x≤
≤x≤ ![]() 或
或 ![]() ≤x≤2.
≤x≤2.
【解析】考查了四边形综合题,涉及的知识点有:坐标轴上点的坐标特征,等腰直角三角形的性质,矩形的性质,分类思想的应用,方程思想的应用,综合性较强,有一定的难度.(1)根据坐标轴上点的坐标特征可求直线l1与x轴,直线l2与AB的交点坐标;(2)分三种情况:①若点A为直角顶点时,点M在第一象限;若点P为直角顶点时,点M在第一象限;③若点M为直角顶点时,点M在第一象限;进行讨论可求点M的坐标;(3)根据矩形的性质可求N点的横坐标x的取值范围.
【考点精析】根据题目的已知条件,利用等腰三角形的性质和矩形的性质的相关知识可以得到问题的答案,需要掌握等腰三角形的两个底角相等(简称:等边对等角);矩形的四个角都是直角,矩形的对角线相等.