题目内容
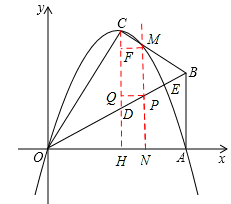
已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA= ,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
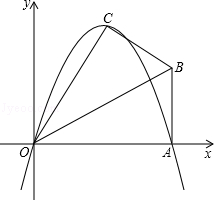
(1)求经过点O,C,A三点的抛物线的解析式.
(2)求抛物线的对称轴与线段OB交点D的坐标.
(3)线段OB与抛物线交与点E,点P为线段OE上一动点(点P不与点O,点E重合),过P点作y轴的平行线,交抛物线于点M,问:在线段OE上是否存在这样的点P,使得PD=CM?若存在,请求出此时点P的坐标;若不存在,请说明理由.
 ,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
(1)求经过点O,C,A三点的抛物线的解析式.
(2)求抛物线的对称轴与线段OB交点D的坐标.
(3)线段OB与抛物线交与点E,点P为线段OE上一动点(点P不与点O,点E重合),过P点作y轴的平行线,交抛物线于点M,问:在线段OE上是否存在这样的点P,使得PD=CM?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(1)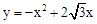
(2)(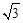 ,1)
,1)
(3)存在。理由见解析
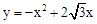
(2)(
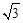 ,1)
,1)(3)存在。理由见解析
分析:(1)在Rt△AOB中,根据AO的长和∠BOA的度数,可求得OB的长,根据折叠的性质即可得到OA=OC,且∠BOC=∠BOA=30°,过C作CD⊥x轴于D,即可根据∠COD的度数和OC的长求得CD、OD的值,从而求出点C、A的坐标,将A、C、O的坐标代入抛物线的解析式中,通过联立方程组即可求出待定系数的值,从而确定该抛物线的解析式。
(2)求出直线BO的解析式,进而利用x=
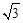 求出y的值,即可得出D点坐标。
求出y的值,即可得出D点坐标。(3)根据(1)所得抛物线的解析式可得到其顶点的坐标(即C点),设直线MP与x轴的交点为N,且PN=t,在Rt△OPN中,根据∠PON的度数,易得PN、ON的长,即可得到点P的坐标,然后根据点P的横坐标和抛物线的解析式可求得M点的纵坐标,过M作MF⊥CD(即抛物线对称轴)于F,过P作PQ⊥CD于Q,若PD=CM,那么CF=QD,根据C、M、P、D四点纵坐标,易求得CF、QD的长,联立两式即可求出此时t的值,从而求得点P的坐标。
解:(1)过点C作CH⊥x轴,垂足为H,

∵在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=
 ,
,∴
 ,AB=2。
,AB=2。由折叠的性质知:∠COB=30°,OC=AO=
 ,
,∴∠COH=60°,OH=
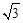 ,CH=3。
,CH=3。∴C点坐标为(
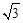 ,3)。
,3)。∵O点坐标为:(0,0),∴抛物线解析式为
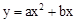 (a≠0)。
(a≠0)。∵图象经过C(
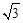 ,3)、A(
,3)、A( ,0)两点,
,0)两点,∴
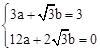 ,解得
,解得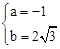 。
。∴此抛物线的函数关系式为:
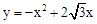 。
。(2)∵AO=
 ,AB=2,∴B点坐标为(
,AB=2,∴B点坐标为( ,2)。
,2)。∴设直线BO的解析式为:y=kx,则2=
 k,解得:k=
k,解得:k=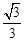 。
。∴设直线BO的解析式为:y=
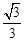 x。
x。∵
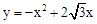 的对称轴为直线
的对称轴为直线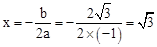 ,
,∴将两函数联立得出:y=
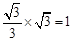 。
。∴抛物线的对称轴与线段OB交点D的坐标为:(
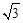 ,1)。
,1)。(3)存在。
∵
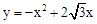 的顶点坐标为(
的顶点坐标为( ,3),即为点C,
,3),即为点C,MP⊥x轴,垂足为N,设PN=t;
∵∠BOA=30°,∴ON=
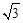 t。∴P(
t。∴P(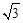 t,t)。
t,t)。作PQ⊥CD,垂足为Q,MF⊥CD,垂足为F,
把x=
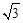 t代入
t代入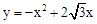 ,得
,得 ,
,∴M(
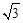 t,﹣
t,﹣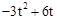 ),F(
),F(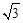 ,
,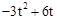 )。
)。同理:Q(
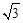 ,t),D(
,t),D(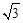 ,1)。
,1)。要使PD=CM,只需CF=QD,即
 ,解得t=
,解得t= ,t=1(舍去)。
,t=1(舍去)。∴P点坐标为
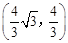 。
。∴存在满足条件的P点,使得PD=CM,此时P点坐标为
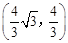

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目

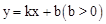 与抛物线
与抛物线 相交于A
相交于A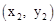 两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且
两点,与x轴正半轴相交于点D,与y轴相交于点C,设△OCD的面积为S,且 。
。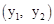 在反比例函数
在反比例函数 的图象上;
的图象上;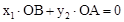 。
。
 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.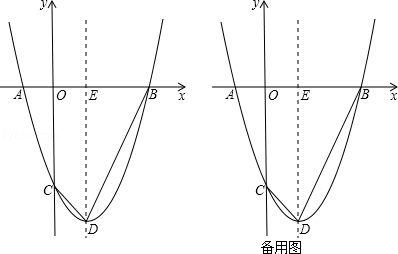
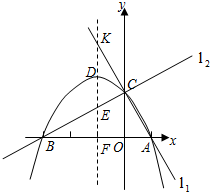
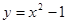 的顶点坐标是( )
的顶点坐标是( ) 的图象如下列四个图之一所示.根据图象分析,a的值等于
的图象如下列四个图之一所示.根据图象分析,a的值等于