题目内容
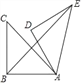
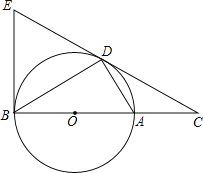
【题目】如图，D为
上一点，点C在直径BA的延长线上，且
．
判断直线CD与的位置关系，并说明理由．
过点B作的切线交CD的延长线于点E，若
，
，求的半径长．
【答案】（1）相切（2）
【解析】分析：
连接OD，根据圆周角定理求出
，求出
，根据切线的判定推出即可；
根据勾股定理求出CE，根据切线长定理求出
，根据相似三角形得出方程，求出方程的解即可．
本题考查了切线的性质和判定，切线长定理，圆周角定理，相似三角形的性质和判定的应用，题目比较典型，综合性比较强，难度适中．
详解：直线CD和
的位置关系是相切，
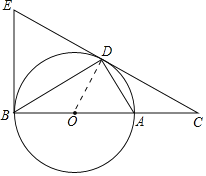
理由是：连接OD，
是的直径，
，
，
，
，
，
，
，
即
，
已知D为的一点，
直线CD是的切线，
即直线CD和的位置关系是相切；
，
，过点B作的切线交CD的延长线于点E，
，
根据切线长定理可得：
，
，
设的半径是x，
，
，
∽
，
，
即
，
解得：
，
即的半径长为．
练习册系列答案
阅读快车系列答案
相关题目
