题目内容
【题目】已知:关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)求证:方程有两个不相等的实数根;
(2)设方程的两个实数根分别为![]() ,
, ![]() (其中
(其中![]() ).若
).若![]() 是关于t的函数,且
是关于t的函数,且![]() ,求这个函数的解析式,并画出函数图象;
,求这个函数的解析式,并画出函数图象;
(3)观察(2)中的函数图象,当![]() 时,写出自变量
时,写出自变量![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() ,画图见解析;(3)当
,画图见解析;(3)当![]() 时,
时, ![]()
【解析】(1)要证明方程有两个不相等的实数根,应从根的判别式入手,只要能够说明根的判别式![]() 即可,这里用到了配方、非负数的性质及题目中的附加条件m>0.
即可,这里用到了配方、非负数的性质及题目中的附加条件m>0.
(2)要求函数![]() 的解析式,需要先求出
的解析式,需要先求出![]() 与
与![]() 的值,由于
的值,由于![]() ,所以方程的根一定是有理数,因此用求根公式可求出方程的根,再代入
,所以方程的根一定是有理数,因此用求根公式可求出方程的根,再代入![]() 中即可.
中即可.
本题解析:(1)证明: ![]() 是关于
是关于![]() 的一元二次方程,
的一元二次方程,
![]() .
.
![]() 当
当![]() 时,
时, ![]() ,即
,即![]() .
.
![]() 方程有两个不相等的实数根.
方程有两个不相等的实数根.
(2)解:由求根公式,得![]() .
.
![]() 或
或![]() .
.
![]() ,
,
![]() .
.
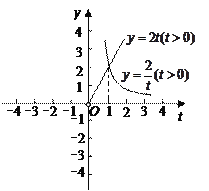
![]() ,
,
![]() ,
, ![]() .
.
![]() .
.
即![]() 为所求.
为所求.
在同一平面直角坐标系中分别画出![]() 与
与![]() 的图象如图.
的图象如图.
(3)由图象可得,当![]() 时,
时, ![]() .
.

练习册系列答案
相关题目