Question

【题目】在Rt△ABC中，∠BAC=90°，D是BC中点，E是AD中点，过A作AF∥BC

①求证：△AEF≌△DEB；

②求证：四边形ADCF是菱形；

③若AB=5，AC=4，求菱形ADCF的面积．

Answer 1

【答案】(1)见解析;(2)10.

【解析】分析: ①根据AAS证△AFE≌△DBE；

②利用①中全等三角形的对应边相等得到AF＝BD．结合已知条件，利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形，由“直角三角形斜边的中线等于斜边的一半”得到AD＝DC，从而得出结论．

③由三角形中线的性质和菱形的性质得出△ABD的面积＝△ACD的面积＝△ACF的面积，得出菱形ADCF的面积＝Rt△ABC的面积＝ABAC，即可得出答案．

详解:

①证明：∵AF∥BC，

∴∠AFE=∠DBE，

∵E是AD的中点，AD是BC边上的中线，

∴AE=DE，BD=CD，

在△AEF和△DEB中，，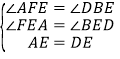

∴△AEF≌△DEB（AAS）；

②证明：由①知，△AFE≌△DBE，则AF=DB．

∵DB=DC，

∴AF=CD．

∵AF∥BC，

∴四边形ADCF是平行四边形，

∵∠BAC=90°，D是BC的中点，E是AD的中点，

∴AD=DC=BC，

∴四边形ADCF是菱形．

③∵D是BC的中点，四边形ADCF是菱形，

∴△ABD的面积=△ACD的面积=△ACF的面积，

∴菱形ADCF的面积=Rt△ABC的面积=ABAC=×5×4=10．

点睛: 本题考查了全等三角形的性质和判定，平行四边形的判定，菱形的判定的应用；熟练掌握菱形与平行四边形的判定，证明三角形全等是解决问题的关键．