题目内容
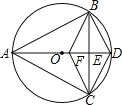
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
【答案】(1)、证明过程见解析;(2)、菱形;理由见解析;(3)、2![]()
【解析】
试题分析:(1)、根据直径得出∠ABD=∠ACD=90°,从而的得出Rt△ABD≌Rt△ACD,然后得出答案;(2)、首先证明△BED≌△CEF,得出CF=BD,即四边形BFCD是平行四边形,根据BD=CD得出菱形;(3)、根据AD是直径,AD⊥BC,BE=CE得出CE2=DEAE,设DE=x,然后求出x的值,根据Rt△CED的勾股定理得出CD的长度.
试题解析:(1)、∵AD是直径, ∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,![]() ∴Rt△ABD≌Rt△ACD, ∴∠BAD=∠CAD,∵AB=AC,∴BE=CE
∴Rt△ABD≌Rt△ACD, ∴∠BAD=∠CAD,∵AB=AC,∴BE=CE
(2)、四边形BFCD是菱形.
∵AD是直径,AB=AC,∴AD⊥BC,BE=CE, ∵CF∥BD,∴∠FCE=∠DBE,
在△BED和△CEF中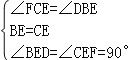 , ∴△BED≌△CEF,∴CF=BD, ∴四边形BFCD是平行四边形,
, ∴△BED≌△CEF,∴CF=BD, ∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,∴BD=CD, ∴四边形BFCD是菱形
(3)、∵AD是直径,AD⊥BC,BE=CE, ∴CE2=DEAE,设DE=x,∵BC=8,AD=10,∴42=x(10﹣x),
解得:x=2或x=8(舍去) 在Rt△CED中,CD=![]() =
=![]() =2
=2![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

