题目内容
【题目】某工程限期完成,甲队单独做正好按期完成,乙队单独做则要延期3天完成.现两队先合作2天,再由乙队单独做,也正好按期完成.如果设规定的期限为x天,那么根据题意可列出方程: 
=1; 
2
=1;③
=1;④
.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】根据规定日期为x天，则甲队完成任务需要x天，乙队完成任务需要(x+3)天.
记该工程总量为“1”，根据题意，得：甲、乙的工作效率分别为
、
.
根据“甲乙合做的工作量+乙做的工作量＝1”，由此可列方程： 
.
根据“甲的工作量+乙做的工作量＝1”，可列方程： 
.
再根据题意得“乙2天做的工作量＝甲3天做的工作量”，可列方程： 
.
综上可知②③④方程均符合题意.
故选C.
点睛: 此题考查了由实际问题抽象出分式方程，关键步骤在于找相等关系．当题中没有一些必须的量时，为了简便，应设其为1．本题要掌握好工作效率，工作总量和工作时间的等量关系．
【题目】中华文明，源远流长：中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：
成绩x/分 | 频数 | 频率 |
50≤x＜60 | 10 | 0.05 |
60≤x＜70 | 20 | 0.10 |
70≤x＜80 | 30 | b |
80≤x＜90 | a | 0.30 |
90≤x≤100 | 80 | 0.40 |
请根据所给信息，解答下列问题：
（1）a= ， b=；
（2）请补全频数分布直方图；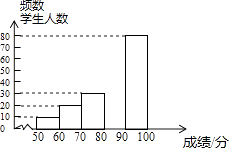 
（3）这次比赛成绩的中位数会落在分数段；
（4）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？