题目内容
【题目】阅读材料:
基本不等式![]() ≤
≤![]() (a>0,b>0),当且仅当a=b时等号成立,它是解决最值问题的有力工具.
(a>0,b>0),当且仅当a=b时等号成立,它是解决最值问题的有力工具.
例如:在x>0的条件下,当x为何值时,x+![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
解:∵x>0,![]() >0∴
>0∴![]() ≥
≥![]() ,即
,即![]() ≥2
≥2![]() ,∴
,∴![]() ≥2
≥2
当且仅当x=![]() ,即x=1时,x+
,即x=1时,x+![]() 有最小值,最小值为2.
有最小值,最小值为2.
请根据阅读材料解答下列问题:
(1)已知x>0,则当x为____时,代数式3x+![]() 的最小值为______;
的最小值为______;
(2)已知a>0,b>0,a2+b2=7,则ab的最大值为_____
(3)已知矩形面积为9,求矩形周长的最小值.
【答案】(1)1,6;(2)![]() ;(3)12.
;(3)12.
【解析】
(1)利用基本不等式即可解决问题;
(2)利用基本不等式变形式即可得解;
(3)设这个矩形的长为x米,则宽=面积÷长,即宽=![]() 米,则矩形周长为2倍的长+2倍的宽,本题就可以转化为两个非负数的和的问题,从而根据基本不等式求解.
米,则矩形周长为2倍的长+2倍的宽,本题就可以转化为两个非负数的和的问题,从而根据基本不等式求解.
解:(1)∵x>0,3x>0,![]() >0,
>0,
∴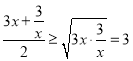 ,
,
即![]() ,
,
当且仅当3x=![]() ,即x=1时,3x+
,即x=1时,3x+![]() 有最小值,最小值为6.
有最小值,最小值为6.
故答案为:1,6;
(2)由基本不等式![]() ≤
≤![]() (a>0,b>0)得
(a>0,b>0)得
![]()
![]()
即![]() (a>0,b>0)
(a>0,b>0)
当且仅当a=b时等号成立,
∵a2+b2=7,
∴![]()
即![]() ,当且仅当a=b=
,当且仅当a=b=![]() 时,等号成立,
时,等号成立,
故答案为:![]() ;
;
(3)设矩形的长为x米,宽=![]() ,矩形的周长为2(
,矩形的周长为2(![]() ),
),
∵x>0,![]() >0,
>0,
∴![]() ,
,
当且仅当![]() 时等号成立,即x=3时,
时等号成立,即x=3时,![]() 有最小值6,2(
有最小值6,2(![]() )有最小值12
)有最小值12
即矩形的周长的最小值为12,此时长为3,宽也为3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目