Question

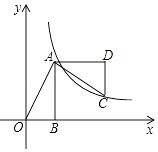
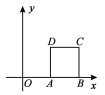
【题目】如图，在平面直角坐标系中，已知A(1，0)，B(2，0)，四边形ABCD是正方形．

(1)写出C，D两点坐标；

(2)将正方形ABCD绕O点逆时针旋转90°后所得四边形的四个顶点的坐标分别是多少？

(3)若将(2)所得的四边形再绕O点逆时针旋转90°后，所得四边形的四个顶点坐标又分别是多少？

Answer 1

【答案】(1)C(2，1)，D(1，1)(2)A(0，1)，B(0，2)，C(－1，2)，D(－1，1)(3)A(－1，0)，B(－2，0)，C(－2，－1)，D(－1，－1)

【解析】

（1）先计算出AB=1，然后利用正方形的性质和点的坐标的表示方法写出C，D两点坐标；
（2）利用正方形和旋转的性质画出正方形ABCD绕O点逆时针旋转90°后所得四边形A′B′C′D′，然后写出四边形A′B′C′D′四个顶点的坐标；
（3）利用正方形和旋转的性质画出正方形A′B′C′D′绕O点逆时针旋转90°后所得四边形A″B″C″D″，然后写出四边形A″B″C″D″四个顶点的坐标．

（1）∵A（1，0），B（2，0），
∴AB=1，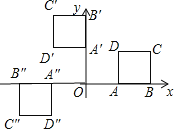
∵四边形ABCD是正方形，
∴AD=BC=CD=1，
∴C（2，1），D（1，1）；
（2）如图，A′（0，1），B′（0，2），C′（-1，2），D′（-1，1）；
（3）如图，A″（-1，0），B″（-2，0），C″（-2，-1），D″（-1，-1）．