题目内容
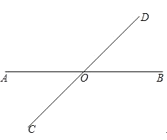
【题目】如图,直线AB、CD相交于点O,∠BOD=45°,按下列要求画图并回答问题:
(1)利用三角尺,在直线AB上方画射线OE,使OE⊥AB;
(2)利用圆规,分别在射线OA、OE上截取线段OM、ON,使OM=ON,连接MN;
(3)利用量角器,画∠AOD的平分线OF交MN于点F;
(4)直接写出∠COF= °.
【答案】(1)见解析;(2)见解析;(3)见解析;(4)112.5
【解析】
(1)利用直角三角尺画OE⊥AB即可;
(2)以O为圆心,任意长为半径画弧交OA、OB于M、N两点,然后连接M、N即可;
(3)利用量角器量出∠AOD的度数,再画出2∠AOD即可得到∠AOF;
(4)由垂直的定义得到∠AOE=∠BOE=90°,再利用∠BOD=45°得到∠COA=45°,∠DOE=45°,所以∠AOD=135°,然后根据角平分线定义得到∠AOF=∠67.5°,从而计算∠COA+∠AOF即可
(1)如图,OE为所作;
(1)如图,MN为所作;
(3)如图,OF为所作;
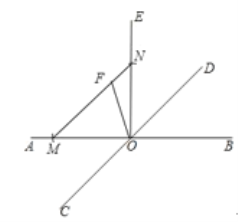
(4)∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∵∠BOD=45°,
∴∠COA=45°,∠DOE=45°,
∴∠AOD=90°+45°=135°,
∵OF平分∠AOD,
∴∠AOF=![]() ×135°=67.5°,
×135°=67.5°,
∴∠COF=45°+67.5°=112.5°.
故答案为112.5°.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目