题目内容
【题目】如图，正方形网格中的每个小正方形边长都是1，每个小格的顶点叫做格点，以格点为顶点分别按下列要求画三角形． 
（1）在图1中，画一个三角形，使它的三边长都是有理数；
（2）在图2中，画一个直角三角形，使它们的三边长都是无理数；
（3）在图3中，画一个正方形，使它的面积是10．
【答案】
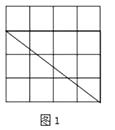
（1）解：三边分别为：3、4、5 （如图1）；
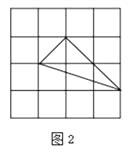
（2）解：三边分别为： 
、2 、 
（如图2）；
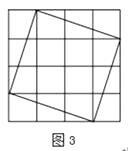
（3）解：画一个边长为 的正方形（如图3）．
【解析】（1）利用勾股定理，找长为有理数的线段，画三角形即可．（2）画一个边长 ，2 ， 的三角形即可；（3）画一个边长为 的正方形即可．
【考点精析】解答此题的关键在于理解无理数的相关知识，掌握在理解无理数时，要抓住“无限不循环”这个要点，归纳起来有四类：（1）开方开不尽的数；（2）有特定意义的数，如圆周率π，或化简后含有π的数；（3）有特定结构的数，如0.1010010001…等；（4）某些三角函数，如sin60o等，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
练习册系列答案
相关题目
