题目内容
【题目】如图，抛物线y=x2﹣3x+ 
与x轴相交于A、B两点，与y轴相交于点C，点D是直线BC下方抛物线上一点，过点D作y轴的平行线，与直线BC相交于点E 
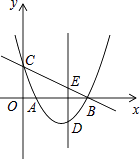
（1）求直线BC的解析式；
（2）当线段DE的长度最大时，求点D的坐标．
【答案】
（1）∵抛物线y=x2﹣3x+ 
与x轴相交于A、B两点，与y轴相交于点C，
∴令y=0，可得x= 
或x= 
，
∴A（ ，0），B（ ，0）；
令x=0，则y= ，
∴C点坐标为（0， ），
设直线BC的解析式为：y=kx+b，则有，
，
解得：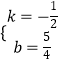 
，
∴直线BC的解析式为：y=- x+ ；
（2）设点D的横坐标为m，则纵坐标为（m， 
），
∴E点的坐标为（m， 
m+ ），
设DE的长度为d，
∵点D是直线BC下方抛物线上一点，
则d= m+ ﹣（m2﹣3m+ ），
整理得，d=﹣m2+ m，
∵a=﹣1＜0，
∴当m= 
= 时，d最大= 
= 
= 
，
∴D点的坐标为（ ，- 
）．
【解析】（1）利用坐标轴上点的特点求出A、B、C点的坐标，再用待定系数法求得直线BC的解析式；（2）设点D的横坐标为m，则纵坐标为（m， ），E点的坐标为（m， 
），可得两点间的距离为d= 
，利用二次函数的最值可得m，可得点D的坐标．此题主要考查了二次函数的性质及其图象与坐标轴的交点，设出D的坐标，利用二次函数最值得D点坐标是解答此题的关键．
【考点精析】根据题目的已知条件，利用二次函数的性质和抛物线与坐标轴的交点的相关知识可以得到问题的答案，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小；一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
