题目内容
如图,∠1=∠2,∠3=∠4
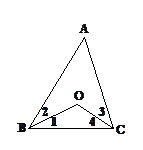
(1)若∠A = 60°,求∠BOC;
(2)若∠A =100°、120°,∠BOC又是多少?
(3)由(1)、(2)你又发现了什么规律?当∠A的度数发生变化后,你的结论仍成立吗?

(1)若∠A = 60°,求∠BOC;
(2)若∠A =100°、120°,∠BOC又是多少?
(3)由(1)、(2)你又发现了什么规律?当∠A的度数发生变化后,你的结论仍成立吗?
(1)120°
(2)150°
(3)成立
证明:(1)
∵∠1=∠2, ∠3=∠4
∠3=∠4
∵∠A=180°-∠1-∠2-∠3-∠4=180°-2(∠1+∠4)
∴∠1+∠4=90°-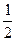 ∠A
∠A
∴ ∠BOC=180°-(∠1+∠4) =180°-(90°-
∠BOC=180°-(∠1+∠4) =180°-(90°-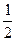 ∠A)= 90°+
∠A)= 90°+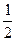 ∠A
∠A
∵∠A=60°
∴∠BOC=180°-(90°-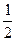 ∠A)= 180°-(90°-
∠A)= 180°-(90°-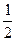 60°)=120°
60°)=120°
(2)由(1)可知∠BOC= 90°+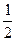 ∠A
∠A
∵∠A =100°
∴∠BOC= 90°+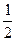 100°=140°
100°=140°
∵∠A =120°
∠BOC= 90°+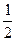 120°=150°
120°=150°
(3)发现了∠BOC= 90°+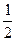 ∠A,当∠A的度数发生变化后,结论仍成立
∠A,当∠A的度数发生变化后,结论仍成立
∵∠1=∠2,
 ∠3=∠4
∠3=∠4 ∵∠A=180°-∠1-∠2-∠3-∠4=180°-2(∠1+∠4)
∴∠1+∠4=90°-
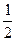 ∠A
∠A∴
 ∠BOC=180°-(∠1+∠4) =180°-(90°-
∠BOC=180°-(∠1+∠4) =180°-(90°-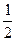 ∠A)= 90°+
∠A)= 90°+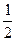 ∠A
∠A∵∠A=60°
∴∠BOC=180°-(90°-
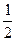 ∠A)= 180°-(90°-
∠A)= 180°-(90°-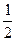 60°)=120°
60°)=120°(2)由(1)可知∠BOC= 90°+
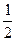 ∠A
∠A∵∠A =100°
∴∠BOC= 90°+
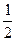 100°=140°
100°=140°∵∠A =120°
∠BOC= 90°+
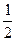 120°=150°
120°=150°(3)发现了∠BOC= 90°+
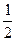 ∠A,当∠A的度数发生变化后,结论仍成立
∠A,当∠A的度数发生变化后,结论仍成立
练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目

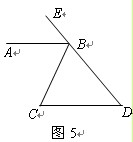
 图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.
图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.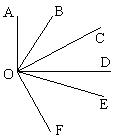
 °)
°)
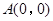 ,
,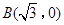 ,
,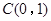 ,在
,在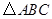 内依次作等边三角形,使其一边在
内依次作等边三角形,使其一边在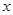 轴上,另一个顶点在
轴上,另一个顶点在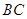 边上,作出的等边三角形分别是第1个
边上,作出的等边三角形分别是第1个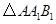 ,第2个
,第2个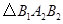 ,第3个
,第3个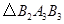 ,…,则第1个等边三角形的边长等于 , 第
,…,则第1个等边三角形的边长等于 , 第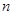 (
( ,且
,且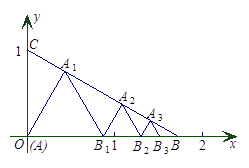
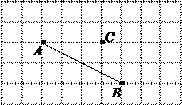
 上的三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离 ( )
上的三点,PA=4cm,PB=5cm,PC=2cm,则点P到直线l的距离 ( )