Question

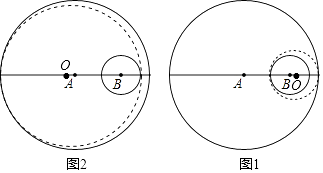
【题目】如图，⊙A和⊙B的半径分别为5和1，AB=3，点O在直线AB上，⊙O与⊙A、⊙B都内切，那么⊙O半径是 ．

Answer 1

【答案】1.5或4.5
【解析】解：设⊙O半径是R，根据题意，分两种情况：

①如图1，OA=5﹣R，OB=R﹣1，

∵OA=AB+OB，

∴5﹣R=3+R﹣1，

解得R=1.5；

②如图2，OA=5﹣R，OB=R﹣1，

∵OA=OB﹣AB，

∴5﹣R=R﹣1﹣3，

解得R=4.5．

所以答案是1.5或4.5．

【考点精析】认真审题，首先需要了解圆与圆的位置关系(两圆之间有五种位置关系：无公共点的，一圆在另一圆之外叫外离，在之内叫内含；有唯一公共点的，一圆在另一圆之外叫外切，在之内叫内切；有两个公共点的叫相交．两圆圆心之间的距离叫做圆心距．两圆的半径分别为R和r，且R≥r，圆心距为P：外离P＞R+r；外切P=R+r；相交R-r＜P＜R+r；内切P=R-r；内含P＜R-r．)．