题目内容
【题目】如图,已知A,B两点的坐标分别为(2 ![]() ,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 .
,0),(0,10),M是△AOB外接圆⊙C上的一点,且∠AOM=30°,则点M的坐标为 . 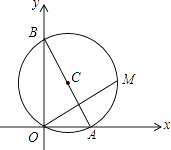
【答案】(4 ![]() ,4).
,4).
【解析】∵A,B两点的坐标分别为(2 ![]() ,0),(0,10),
,0),(0,10),
∴OB=10,OA=2 ![]() ,
,
∴AB= ![]() =4
=4 ![]() ,
,
∵∠AOB=90°,
∴AB是直径,CM=2 ![]() ,
,
∴Rt△AOB外接圆的圆心为AB中点,
∴C点坐标为( ![]() ,5),
,5),
过点C作CF∥OA,过点M作ME⊥OA于E交CF于F,作CN⊥OE于N,如图所示:
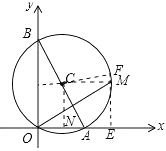
则ON=AN= ![]() OA=
OA= ![]() ,
,
设ME=x,
∵∠AOM=30°,
∴OE= ![]() x
x
∴∠CFM=90°,
∴MF=5﹣x,CF= ![]() x﹣
x﹣ ![]() ,CM=2
,CM=2 ![]() ,
,
在△CMF中,根据勾股定理得:( ![]() x﹣
x﹣ ![]() )2+(5﹣x)2=(2
)2+(5﹣x)2=(2 ![]() )2,
)2,
解得:x=4或x=0(舍去),
∴OE= ![]() x=4
x=4 ![]()
所以答案是:(4 ![]() ,4).
,4).
【考点精析】解答此题的关键在于理解圆周角定理的相关知识,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半.

练习册系列答案
相关题目
【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | … |
销售额/元 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | … |
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用![]() 表示橘子卖出的质量,
表示橘子卖出的质量,![]() 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系,![]() 与
与![]() 之间的关系式为______.
之间的关系式为______.
(4)当橘子的销售额是100元时,共卖出多少千克橘子?