题目内容
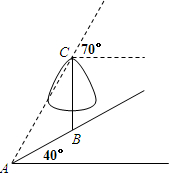 如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)
如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)(参考数据:sin20°=0.34,tan20°=0.36,sin30°=0.50,tan30°=0.58,sin40°=0.64,tan40°=0.84,sin70°=0.94,tan70°=2.75)
分析:本题可通过构造直角三角形来解答,过B点作BD⊥AC,D为垂足,在直角三角形BCD中,已知BC的长,可求∠BCD的度数,那么可求出BD的长,在直角三角形ABD中,可求∠DAB=70°-40°=30°,前面又得到了BD的长,那么就可求出AB的长.
解答: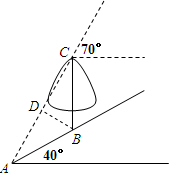 解:过B点作BD⊥AC,D为垂足,
解:过B点作BD⊥AC,D为垂足,
在直角三角形BCD中,∠BCD=180°-70°-90°=20°,
BD=BC•sin20°=4×0.34=1.36米,
在直角三角形ABD中,∠DAB=70°-40°=30°,
AB=BD÷sin30°=1.36÷
≈2.7米.
答:树影AB的长约为2.7米.
 解:过B点作BD⊥AC,D为垂足,
解:过B点作BD⊥AC,D为垂足,在直角三角形BCD中,∠BCD=180°-70°-90°=20°,
BD=BC•sin20°=4×0.34=1.36米,
在直角三角形ABD中,∠DAB=70°-40°=30°,
AB=BD÷sin30°=1.36÷
| 1 |
| 2 |
答:树影AB的长约为2.7米.
点评:本题是将实际问题转化为直角三角形中的数学问题,可通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题解决.

练习册系列答案
相关题目
 得该树在斜坡上的树影BC的长为8m,
得该树在斜坡上的树影BC的长为8m,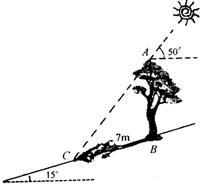 24、如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成50°时,测得该树在斜坡上的树影BC的长为7m,求树高.(精确到0.1m)
24、如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成50°时,测得该树在斜坡上的树影BC的长为7m,求树高.(精确到0.1m) 如图,在一个坡角为30°的斜坡上有一棵树,高AB,当太阳光与水平线成60°时,测得该树在斜坡上的树影BC的长为6m,则树高AB=
如图,在一个坡角为30°的斜坡上有一棵树,高AB,当太阳光与水平线成60°时,测得该树在斜坡上的树影BC的长为6m,则树高AB=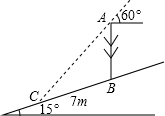 (A)如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成60°时.测得该树在斜坡上的树影BC的长为7m,则树高为
(A)如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成60°时.测得该树在斜坡上的树影BC的长为7m,则树高为