题目内容
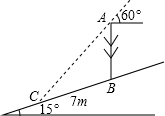 (A)如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成60°时.测得该树在斜坡上的树影BC的长为7m,则树高为
(A)如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成60°时.测得该树在斜坡上的树影BC的长为7m,则树高为7
| 2 |
7
m.(保留根号) | 2 |
(B)如果α、β是一元二次方程x2+3x-1=0的两个根,那么α2+2α-β的值是
4
4
.分析:(A)在△ABC中易求得∠ACB=45°,∠BAC=30°.已知BC=7,解此三角形求AB.作BD⊥AC于D,解直角三角形求解.
(B)根据α、β是一元二次方程x2+3x-1=0的两个根得到α+β=-3,α2+αx=1,将α2+2α-β变形为α2+3α-(α+β)后代入即可求值.
(B)根据α、β是一元二次方程x2+3x-1=0的两个根得到α+β=-3,α2+αx=1,将α2+2α-β变形为α2+3α-(α+β)后代入即可求值.
解答: 解:(A)作BD⊥AC于点D.易得∠ACB=45°,∠CAB=30°.
解:(A)作BD⊥AC于点D.易得∠ACB=45°,∠CAB=30°.
∵BC=7.
∴BD=
.
∴AB=2DB=7
(m).
(B)∵α、β是一元二次方程x2+3x-1=0的两个根,
∴α+β=-3,α2+3α=1,
∴α2+2α-β=α2+3α-(α+β)=1-(-3)=4
故答案为7
,4.
 解:(A)作BD⊥AC于点D.易得∠ACB=45°,∠CAB=30°.
解:(A)作BD⊥AC于点D.易得∠ACB=45°,∠CAB=30°.∵BC=7.
∴BD=
7
| ||
| 2 |
∴AB=2DB=7
| 2 |
(B)∵α、β是一元二次方程x2+3x-1=0的两个根,
∴α+β=-3,α2+3α=1,
∴α2+2α-β=α2+3α-(α+β)=1-(-3)=4
故答案为7
| 2 |
点评:本题考查了解直角三角形及一元二次方程的有关知识,对于此类问题常常转化成直角三角形,可利用三角函数知识、勾股定理或相似三角形的知识来解决,而(B)中利用根与系数的关系进行变形是解题的关键.

练习册系列答案
相关题目
 如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值:
如图,在一个坡角为30°的斜坡上有一电线杆AB,当太阳光与水平线成45°角时,测得该杆在斜坡上的影长BC为20m.求电线杆AB的高(精确到0.1m,参考数值: 20、如图,在一个坡角为20°的斜坡上有一棵树,高为AB,当太阳光线与水平线成52°角时,测得该树斜坡上的树影BC的长为10m,求树高AB(精确到0.1m)
20、如图,在一个坡角为20°的斜坡上有一棵树,高为AB,当太阳光线与水平线成52°角时,测得该树斜坡上的树影BC的长为10m,求树高AB(精确到0.1m)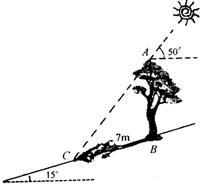 24、如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成50°时,测得该树在斜坡上的树影BC的长为7m,求树高.(精确到0.1m)
24、如图,在一个坡角为15°的斜坡上有一棵树,高为AB.当太阳光与水平线成50°时,测得该树在斜坡上的树影BC的长为7m,求树高.(精确到0.1m)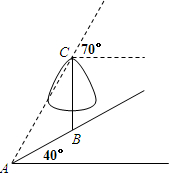 如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)
如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)