题目内容
 在同一平面直角坐标系中有5个点:A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(0,-3).
在同一平面直角坐标系中有5个点:A(1,1),B(-3,-1),C(-3,1),D(-2,-2),E(0,-3).(1)画出△ABC的外接圆⊙P,并指出点D与⊙P的位置关系;
(2)若直线l经过点D(-2,-2),E(0,-3),判断直线l与⊙P的位置关系.
【答案】分析:(1)在直角坐标系内描出各点,画出△ABC的外接圆,并指出点D与⊙P的位置关系即可;
(2)连接PE,用待定系数法求出直线PD与PE的位置关系即可.
解答:解:(1)如图所示:
△ABC外接圆的圆心为(-1,0),点D在⊙P上;
(2)方法一:连接PD,
设过点P、D的直线解析式为y=kx+b,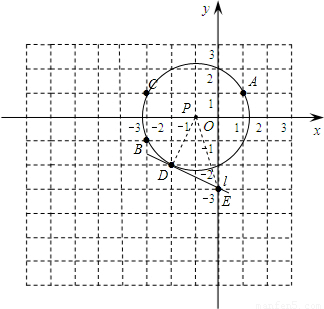
∵P(-1,0)、D(-2,-2),
∴ ,
,
解得 ,
,
∴此直线的解析式为y=2x+2;
设过点D、E的直线解析式为y=ax+c,
∵D(-2,-2),E(0,-3),
∴ ,
,
解得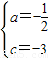 ,
,
∴此直线的解析式为y=- x-3,
x-3,
∵2×(- )=-1,
)=-1,
∴PD⊥DE,
∵点D在⊙P上,
∴直线l与⊙P相切.
方法二:连接PE,PD,
∵直线 l过点 D(-2,-2 ),E (0,-3 ),
∴PE2=12+32=10,PD2=5,DE2=5,..
∴PE2=PD2+DE2.
∴△PDE 是直角三角形,且∠PDE=90°.
∴PD⊥DE.
∵点D在⊙P上,
∴直线l与⊙P相切.
点评:本题考查的是直线与圆的位置关系,根据题意画出图形,利用数形结合求解是解答此题的关键.
(2)连接PE,用待定系数法求出直线PD与PE的位置关系即可.
解答:解:(1)如图所示:
△ABC外接圆的圆心为(-1,0),点D在⊙P上;
(2)方法一:连接PD,
设过点P、D的直线解析式为y=kx+b,

∵P(-1,0)、D(-2,-2),
∴
 ,
,解得
 ,
,∴此直线的解析式为y=2x+2;
设过点D、E的直线解析式为y=ax+c,
∵D(-2,-2),E(0,-3),
∴
 ,
,解得
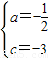 ,
,∴此直线的解析式为y=-
 x-3,
x-3,∵2×(-
 )=-1,
)=-1,∴PD⊥DE,
∵点D在⊙P上,
∴直线l与⊙P相切.
方法二:连接PE,PD,
∵直线 l过点 D(-2,-2 ),E (0,-3 ),
∴PE2=12+32=10,PD2=5,DE2=5,..
∴PE2=PD2+DE2.
∴△PDE 是直角三角形,且∠PDE=90°.
∴PD⊥DE.
∵点D在⊙P上,
∴直线l与⊙P相切.
点评:本题考查的是直线与圆的位置关系,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
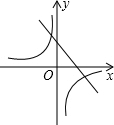
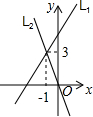 直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )
直线L1:y=2x+5与直线L2:y=kx+b在同一平面直角坐标系中的图象如图,则关于x的不等式2x+5<kx+b的解集为( )