题目内容
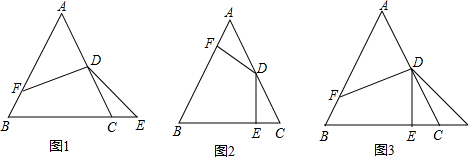
 如图,D是等边△ABC的边AC的中点,点E在BC的延长线上,CE=CD,若S△ABC=
如图,D是等边△ABC的边AC的中点,点E在BC的延长线上,CE=CD,若S△ABC= cm2,则△BDE的周长是________.
cm2,则△BDE的周长是________.
(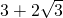 )cm
)cm
分析:根据三角形ABC为等边三角形,得到三边相等,三个内角都为60°,由D为AC中点,根据“三线合一”得到BD与AC垂直,且∠ABD=∠CBD=30°,然后在直角三角形BCD中,根据30°角所对的直角边等于斜边的一半得到CD为BC的一半,然后再由CE=CD,根据“等边对等角”得到∠CDE=∠E,因为∠ACB为三角形DCE的外角,根据外角性质得到∠CDE=∠E=30°,进而利用等量代换得到∠DBE=∠E,根据“等角对等边”得到DB=DE,设CD为x,则BC=AC=2x,根据勾股定理表示出BD,利用三角形的面积公式表示出三角形ABC的面积,让面积等于已知的 列出关于x的方程,求出方程的解即可得到x的值,进而得到BD,DE,BC及CE的长,四条边相加即可得到周长.
列出关于x的方程,求出方程的解即可得到x的值,进而得到BD,DE,BC及CE的长,四条边相加即可得到周长.
解答:∵D是等边△ABC的边AC的中点,
∴BD⊥AC,∠DBC=∠DBA= ∠ABC=30°,
∠ABC=30°,
∴CD= BC,
BC,
∵CE=CD,∴∠CDE=∠E,
又∵等边三角形ABC,
∴∠ACB=60°,且为△CDE的外角,
∴∠CDE=∠E=30°,
∴∠DBC=∠E,
∴DB=DE,
设CD=x,则BC=AC=AB=2x,
根据勾股定理得:BD= x,
x,
则S△ABC= AC•BD=
AC•BD= ×2x×
×2x× x=
x= ,
,
解得:x=1,即CD=CE=1,BC=2,BD= ,
,
△BDE的周长=BD+DE+BE=2BD+BC+CE=(3+2 )cm.
)cm.
故答案为:(3+2 )cm.
)cm.
点评:此题考查了等边三角形的性质,直角三角形的性质及三角形外角性质.将直角三角形的三边用含有同一个字母的代数式表示,利用勾股定理列方程求解是本题的关键.通过此题,让学生明白计算的方法也是研究几何图形性质,完成几何证明的有效途径之一.
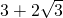 )cm
)cm分析:根据三角形ABC为等边三角形,得到三边相等,三个内角都为60°,由D为AC中点,根据“三线合一”得到BD与AC垂直,且∠ABD=∠CBD=30°,然后在直角三角形BCD中,根据30°角所对的直角边等于斜边的一半得到CD为BC的一半,然后再由CE=CD,根据“等边对等角”得到∠CDE=∠E,因为∠ACB为三角形DCE的外角,根据外角性质得到∠CDE=∠E=30°,进而利用等量代换得到∠DBE=∠E,根据“等角对等边”得到DB=DE,设CD为x,则BC=AC=2x,根据勾股定理表示出BD,利用三角形的面积公式表示出三角形ABC的面积,让面积等于已知的
 列出关于x的方程,求出方程的解即可得到x的值,进而得到BD,DE,BC及CE的长,四条边相加即可得到周长.
列出关于x的方程,求出方程的解即可得到x的值,进而得到BD,DE,BC及CE的长,四条边相加即可得到周长.解答:∵D是等边△ABC的边AC的中点,
∴BD⊥AC,∠DBC=∠DBA=
 ∠ABC=30°,
∠ABC=30°,∴CD=
 BC,
BC,∵CE=CD,∴∠CDE=∠E,
又∵等边三角形ABC,
∴∠ACB=60°,且为△CDE的外角,
∴∠CDE=∠E=30°,
∴∠DBC=∠E,
∴DB=DE,
设CD=x,则BC=AC=AB=2x,
根据勾股定理得:BD=
 x,
x,则S△ABC=
 AC•BD=
AC•BD= ×2x×
×2x× x=
x= ,
,解得:x=1,即CD=CE=1,BC=2,BD=
 ,
,△BDE的周长=BD+DE+BE=2BD+BC+CE=(3+2
 )cm.
)cm.故答案为:(3+2
 )cm.
)cm.点评:此题考查了等边三角形的性质,直角三角形的性质及三角形外角性质.将直角三角形的三边用含有同一个字母的代数式表示,利用勾股定理列方程求解是本题的关键.通过此题,让学生明白计算的方法也是研究几何图形性质,完成几何证明的有效途径之一.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
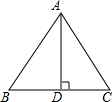 如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于
如图,△ABC是等边三角形,AB=4cm,则BC边上的高AD等于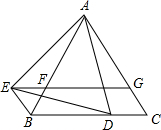 如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE.
如图,△ABC是等边三角形,点D是线段BC上的一个动点(点D不与点B、C重合),△ADE是以AD为边的等边三角形,过点E作BC的平行线,分别交AB、AC于点F、G,连接BE.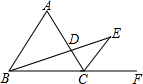 如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.
如图,△ABC是等边三角形,CE是外角平分线,点D在AC上,连结BD并延长与CE交于点E.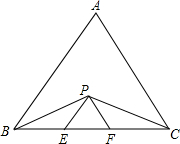 如图,△ABC是等边三角形,P为△ABC内任意一点,PE∥AB,PF∥AC.那么,△PEF是什么三角形?说明理由.
如图,△ABC是等边三角形,P为△ABC内任意一点,PE∥AB,PF∥AC.那么,△PEF是什么三角形?说明理由.