��Ŀ����
����Ŀ����֪����MON=40����OEƽ�֡�MON����A��B��C�ֱ�������OM��OE��ON�ϵĶ��㣨A��B��C�����O �غϣ�������AC������OE�ڵ�D�����OAC=x����

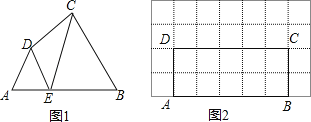
��1����ͼ1����AB��ON����١�ABO�Ķ����� ��
�ڵ���BAD=��ABDʱ��x= ������BAD=��BDAʱ��x= ��
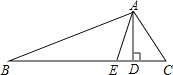
��2����ͼ2����AB��OM�����Ƿ����������x��ֵ��ʹ����ADB����������ȵĽǣ������ڣ����x��ֵ���������ڣ�˵�����ɣ�
���𰸡�������
��������������������ý�ƽ���ߵ����������ABO�Ķ����ǹؼ����������۵�˼�룮
�⣺��1���١ߡ�MON=40����OEƽ����MON���AOB=��BON=20��
��AB��ON���ABO=20��
�ڡߡ�BAD=��ABD���BAD=20��ߡ�AOB+��ABO+��OAB=180����OAC=120��
�ߡ�BAD=��BDA����ABO=20����BAD=80��ߡ�AOB+��ABO+��OAB=180����OAC=60��
�ʴ�Ϊ����20 ��120��60
��2��������D���߶�OB��ʱ��
����BAD=��ABD����x=20
����BAD=��BDA����x=35
����ADB=��ABD����x=50
������D������BE��ʱ����Ϊ��ABE=110�����������ε��ڽǺ�Ϊ180����
����ֻ����BAD=��BDA����ʱx=125��
���Ͽ�֪������������x��ֵ��ʹ����ADB����������ȵĽǣ�
��x=20��35��50��125��

 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�