题目内容
【题目】如图,⊙O的半径为17cm,弦AB∥CD,AB=30cm,CD=16cm,圆心O位于AB,CD的上方,求AB和CD的距离. 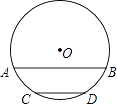
【答案】解:过点O作弦AB的垂线,垂足为E,延长OE交CD于点F,连接OA,OC, ∵AB∥CD,
∴OF⊥CD,
∵AB=30cm,CD=16cm,
∴AE= ![]() AB=
AB= ![]() ×30=15cm,CF=
×30=15cm,CF= ![]() CD=
CD= ![]() ×16=8cm,
×16=8cm,
在Rt△AOE中,
OE= ![]() =
= ![]() =8cm,
=8cm,
在Rt△OCF中,
OF= ![]() =
= ![]() =15cm,
=15cm,
∴EF=OF﹣OE=15﹣8=7cm.
答:AB和CD的距离为7cm.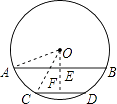
【解析】过点O作弦AB的垂线,垂足为E,延长AE交CD于点F,连接OA,OC;由于AB∥CD,则OF⊥CD,EF即为AB、CD间的距离;由垂径定理,易求得AE、CF的长,在构建的直角三角形中,根据勾股定理即可求出OE、OF的长,也就求出了EF的长,即弦AB、CD间的距离.
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对垂径定理的理解,了解垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.

 全优点练单元计划系列答案
全优点练单元计划系列答案【题目】某社区准备在甲乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩绘制了尚不完整的统计图表,并计算了甲成绩的平均数和方差(见小宇的作业).
甲、乙两人射箭成绩统计表
第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
甲成绩 | 9 | 4 | 7 | 4 | 6 |
乙成绩 | 7 | 5 | 7 | a | 7 |
(1)a= , ![]() =;
=;
(2)请完成图中表示乙成绩变化情况的折线;
(3)①观察图,可看出的成绩比较稳定(填“甲”或“乙”).参照小宇的计算方法,计算乙成绩的方差,并验证你的判断.
②请你从平均数和方差的角度分析,谁将被选中.
【题目】某面粉加工厂加工的面粉,用每袋可装10g面粉的袋子装了200袋经过称重,质量超过标准质量10kg的用正数表示,质量低于标准质量10kg的用负数表示,结果记录如下
与标准质量的偏差(kg) | ﹣1.5 | ﹣1 | ﹣0.5 | 0 | 0.5 | 1 | 2 |
袋数(袋) | 40 | 30 | 10 | 25 | 40 | 20 | 35 |
(1)求这批面粉的总质量;
(2)如果100kg小麦加工80kg面粉,那么这批面粉是由多少千克小麦加工的?