题目内容
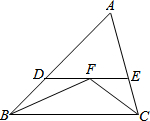
如图所示，已知△ABC中，OB、OC分别是∠B，∠C的平分线，过点O作MN∥BC，若AB=12，BC=24，AC=18，则△AMN的周长为______．
∵OB平分∠ABC，
∴∠ABO=∠OBC，
∵MN∥BC，
∴∠OBC=∠BOM，
∴∠ABO=∠BOM，
∴BM=OM，
同理可得CN=ON，
∴△AMN的周长=AM+MO+ON+AN=AM+BM+CN+AN=AB+AC，
∵AB=12，AC=18，
∴△AMN的周长=12+18=30．
故答案为：30．
∴∠ABO=∠OBC，
∵MN∥BC，
∴∠OBC=∠BOM，
∴∠ABO=∠BOM，
∴BM=OM，
同理可得CN=ON，
∴△AMN的周长=AM+MO+ON+AN=AM+BM+CN+AN=AB+AC，
∵AB=12，AC=18，
∴△AMN的周长=12+18=30．
故答案为：30．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
