题目内容
【题目】已知抛物线的解析式为y=﹣ 
x2+bx+5．
（1）当自变量 x≥2时，函数值y 随 x的增大而减少，求b 的取值范围；
（2）如图，若抛物线的图象经过点A（2，5），与x 轴交于点C，抛物线的对称轴与x 轴交于B．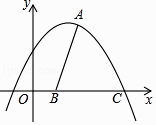
①求抛物线的解析式；
②在抛物线上是否存在点P，使得∠PAB=∠ABC？若存在，求出点P 的坐标；若不存在，请说明理由．
【答案】
（1）
解：抛物线的对称轴为：x=10b，
由题意可知：x≥2时，函数值y 随 x的增大而减少，
∴10b≤2，
∴b≤ 
（2）
解：①将A（2，5）代入抛物线的解析式中，
∴5=﹣ 
×4+2b+5，
∴b= 
，
∴抛物线的解析式为：y=﹣ x2+ x+5，
②由于∠PAB=∠ABC，
当P在对称轴的左侧时，
此时∠PAB=∠ABC，
∴PA∥BC，
∴P的纵坐标与A的纵坐标相同，
∴P（0，5），
当P在对称轴的右侧时，
连接AP并延长交x轴于E，
此时∠PAB=∠ABC
∴AE=BE，
过点A作AG⊥x轴于点G，过点P作PH⊥x轴于点H，过点E作EF⊥AB于点F，
∵B（1，0），A（2，5），
∴AG=5，BG=1，
∴由勾股定理可知：AB= 
，
∵AE=BE，EF⊥AB，
∴BF= 
AB= 
，
∵cos∠ABC= 
= 
，
∴cos∠ABC= 
= ，
∴BE=13，
∴GE=BE﹣BG=12，
∴tan∠PEG= 
= 
，
设P（x，﹣ x2+ x+5），
∵E（14，0），
∴HE=14﹣x，PH=﹣ x2+ x+5，
∴tan∠PEG= 
= ，
即 
= ，
解得：x=2（舍去）或x= 
，
∴P（ ， 
）
综上所述，P（0，5）或P（ ， ）
【解析】（1）由题意可知：对称轴只需要小于或等于2即可，从而可求出b的范围；（2）①将A代入抛物线解析式即可求出b的值．②由于∠PAB=∠ABC，且P在抛物线上，故需要对P的位置进行分类讨论即可．
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识，掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小，以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．
